题目内容
设直角三角形的两条直角边的长分别为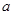 ,b,斜边长为c,斜边上的高为h,则有
,b,斜边长为c,斜边上的高为h,则有
①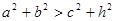 , ②
, ②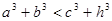 ,
,
③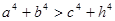 , ④
, ④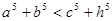 .
.
其中正确结论的序号是 ;进一步类比得到的一般结论是 .
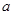 ,b,斜边长为c,斜边上的高为h,则有
,b,斜边长为c,斜边上的高为h,则有①
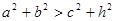 , ②
, ②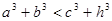 ,
, ③
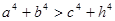 , ④
, ④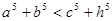 .
.其中正确结论的序号是 ;进一步类比得到的一般结论是 .
②④
由a+b<c+h成立,我们可以类比给出a3+b3<c3+h3;a4+b4<c4+h4;a5+b5<c5+h5等,再逐一分析它们的真假,再根据其中的规律,归纳猜想出一般性的结论.
解:在直角三角形ABC中,a=csinA,b=ccosA,ab=ch,所以h=csinAcosA.
于是an+bn=cn(sinnA+cosnA),cn+hn=cn(1+sinnAcosnA).an+bn-cn-hn=cn(sinnA+cosnA-1-sinnAcosnA)=cn(sinnA-1)(1-cosnA)<0.
所以an+bn<cn+hn(n∈N*).
故正确答案是②④;结论是an+bn<cn+hn(n∈N*)。
解:在直角三角形ABC中,a=csinA,b=ccosA,ab=ch,所以h=csinAcosA.
于是an+bn=cn(sinnA+cosnA),cn+hn=cn(1+sinnAcosnA).an+bn-cn-hn=cn(sinnA+cosnA-1-sinnAcosnA)=cn(sinnA-1)(1-cosnA)<0.
所以an+bn<cn+hn(n∈N*).
故正确答案是②④;结论是an+bn<cn+hn(n∈N*)。

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 :
: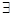 x
x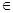 R,
R, 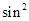
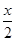 +
+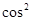
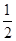
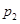 :
: 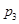 :
: 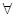 x
x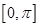 ,
,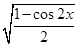 =sinx
=sinx 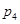 : sinx=cosy
: sinx=cosy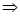 x+y=
x+y=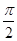
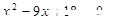 ”,那么它的的逆命题、否命题与逆否命题这三个命题中,真命题的个数有
”,那么它的的逆命题、否命题与逆否命题这三个命题中,真命题的个数有 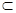 α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b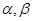 为互不重合的平面,
为互不重合的平面,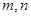 为互不重合的直线,给出下列四个命题:
为互不重合的直线,给出下列四个命题: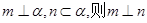 ; ②若
; ②若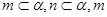 ∥
∥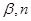 ∥
∥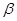 ,则
,则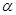 ∥
∥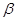 ;
;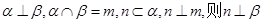 ; ④若
; ④若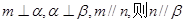 .
.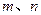 和平面
和平面 .给出下面三个命题:
.给出下面三个命题: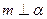 ,
,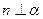
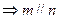 ;②
;②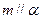 ,
,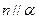
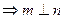 .
. 其中真命题的序号有 .(写出你认为所有真命题的序号)
其中真命题的序号有 .(写出你认为所有真命题的序号)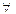
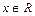 ,
,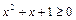 ; ②
; ②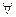
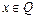 ,
,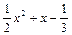 是有理数;
是有理数;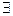
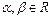 ,使
,使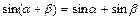 ;④
;④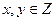 ,使
,使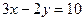 。
。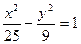 与椭圆
与椭圆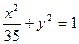 有相同的焦点;
有相同的焦点;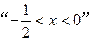 是“2x2-5x-3<0”必要不充分条件;
是“2x2-5x-3<0”必要不充分条件;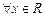 ,
,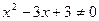 .
.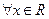 ,
,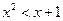
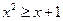
 ,
,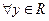 ,
,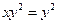
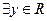 ,
,