题目内容
计算:
(1)已知x>0,化简(2x
+3
)(2x
-3
)-4x-
(x-x
)
(2)log2.56.25+lg
+ln
+21+log23.
(1)已知x>0,化简(2x
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)log2.56.25+lg
| 1 |
| 100 |
| e |
分析:(1)利用分数指数幂的运算法则化简要求的式子,得出结果.
(2)根据对数的运算性质化简要求的式子为log2.52.52+lg10-2+lne
+2×2log23,进一步化简求得结果.
(2)根据对数的运算性质化简要求的式子为log2.52.52+lg10-2+lne
| 1 |
| 2 |
解答:解:(1)(2x
+3
)(2x
-3
)-4x-
(x-x
)
=(2x
)2-(3
)2-4x-
•x+4x-
•x
…(3分)
=4x
-33-4x
+4…(5分)
=-23.…(6分)
(2)log2.56.25+lg
+ln
+21+log23=log2.52.52+lg10-2+lne
+2×2log23…(9分)
=2-2+
+2×3 …(12分)
=6
.…(13分)
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=(2x
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4x
| 1 |
| 2 |
| 1 |
| 2 |
=-23.…(6分)
(2)log2.56.25+lg
| 1 |
| 100 |
| e |
| 1 |
| 2 |
=2-2+
| 1 |
| 2 |
=6
| 1 |
| 2 |
点评:本题主要考查分数指数幂的运算法则,对数的运算性质的应用,属于基础题.

练习册系列答案
相关题目

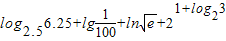 .
. 的值;
的值; 
 .
.