题目内容
计算:
(1)已知x+x-1=3,求x
+x-
的值;
(2)(lg2)2+lg5×lg20.
(1)已知x+x-1=3,求x
| 1 |
| 2 |
| 1 |
| 2 |
(2)(lg2)2+lg5×lg20.
分析:(1)将要求的式子平方即可求出;
(2)利用lg2+lg5=1即可求出.
(2)利用lg2+lg5=1即可求出.
解答:解:(1)∵(x
+x-
)2=x+2+x-1=3+2=5,且x
+x-
>0,∴x
+x-
=
;
(2)原式=lg22+lg5(lg2+1)=lg2(lg2+lg5)+lg5=lg2+lg5=1.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
(2)原式=lg22+lg5(lg2+1)=lg2(lg2+lg5)+lg5=lg2+lg5=1.
点评:熟练掌握指数幂的运算性质和对数的运算性质是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

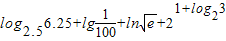 .
. 的值;
的值; 
 .
.