题目内容
求函数解析式(1)求一次函数f(x),使f[f(x)]=9x+1;
(2)已知f(
| x+1 |
| x |
| x2+x+1 |
| x2 |
(3)f(x)是奇函数,g(x)是偶函数,并且f(x)+g(x)=
| 1 |
| x-1 |
(4)f(x)的定义域是正整数集N*,f(1)=1,且f(x+1)=f(x)+5,求f(x).
分析:(1)可用待定系数法;(2)可用配凑法;(3)因考虑到f(x)是奇函数,g(x)是偶函数,所以可以用-x代换x,利用方程组法求解;(4)转换为数列问题,利用数列的方法解决问题.
解答:解:(1)令f(x)=ax+b,则f[f(x)]=a(ax+b)+b=a2x+ab+b=9x+1;
解得:
或
∴f(x)=3x+
或f(x)=-3x-
(2)∵f(
)=
=(
)2-(
)+1
∴f(x)=x2-x+1(x≠1)
(3)∵f(x)是奇函数,g(x)是偶函数,且f(x)+g(x)=
①,
∴f(-x)+g(-x)=-f(x)+g(x)=
②,
即:f(x)=
; g(x)=
(4)∵f(x+1)=f(x)+5,∴f(x+1)-f(x)=5,
∴f(x)-f(x-1)=5,
f(x-1)-f(x-2)=5,
…
f(3)-f(2)=5,
f(2)-f(1)=5,
将上边一系列式子左右两边相加得f(x)-f(1)=5(x-1),又∵f(1)=1,
∴f(x)=5x-4
解得:
|
|
∴f(x)=3x+
| 1 |
| 4 |
| 1 |
| 2 |
(2)∵f(
| x+1 |
| x |
| x2+x+1 |
| x2 |
| x+1 |
| x |
| x+1 |
| x |
∴f(x)=x2-x+1(x≠1)
(3)∵f(x)是奇函数,g(x)是偶函数,且f(x)+g(x)=
| 1 |
| x-1 |
∴f(-x)+g(-x)=-f(x)+g(x)=
| 1 |
| -x-1 |
即:f(x)=
| x |
| x2-1 |
| 1 |
| x2-1 |
(4)∵f(x+1)=f(x)+5,∴f(x+1)-f(x)=5,
∴f(x)-f(x-1)=5,
f(x-1)-f(x-2)=5,
…
f(3)-f(2)=5,
f(2)-f(1)=5,
将上边一系列式子左右两边相加得f(x)-f(1)=5(x-1),又∵f(1)=1,
∴f(x)=5x-4
点评:求解析式的几种常见方法:①代入法:即已知f(x),g(x),求f(g(x))用代入法,只需将g(x)替换f(x)中的x即得;②换元法:已知f(g(x)),g(x),求f(x)用换元法,令g(x)=t,解得x=g-1(t),然后代入f(g(x))中即得f(t),从而求得f(x).当f(g(x))的表达式较简单时,可用“配凑法”;③待定系数法:当函数f(x)类型确定时,可用待定系数法.④方程组法:方程组法求解析式的实质是用了对称的思想.一般来说,当自变量互为相反数、互为倒数或是函数具有奇偶性时,均可用此法.在解关于f(x)的方程时,可作恰当的变量代换,列出f(x)的方程组,求得f(x).

练习册系列答案
相关题目
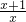 )=
)=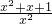 ,求f(x);
,求f(x); ,求f(x)、g(x);
,求f(x)、g(x);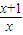 )=
)=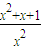 ,求f(x);
,求f(x);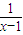 ,求f(x)、g(x);
,求f(x)、g(x);