题目内容
幂指函数
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
。运用此方法可以探求得知
的一个单调递增区间为（ ）
| A．(0,2) | B．(2,3) | C．(e,4) | D．(3,8) |
A
解析试题分析：由题意可知
，令
，可以解得
，所以A是一个单调区间.
考点：本小题主要考查新定义下函数的求导和利用导数求单调区间，考查学生类比的能力和运算求解能力.
点评：新定义问题要仔细读题，根据新定义把问题转化为熟悉的题型来解决，此类问题一般难度不大.
练习册系列答案
小学教材完全解读系列答案
相关题目
函数y=(2k+1)x+b在(-∞,+∞)上是减函数，则（ ）
A．k> | B．k< | C．k> | D．k< |
数
的定义域是（ ）
A． | B． | C． | D． |
已知函数
,
,
，
，
（ ）
A． | B． | C． | D． |
已知：
在
上为减函数，则
的取值范围为（ ）。
A． | B． | C． | D． |
已知二次函数
的导数为
，
，对于任意实数
都有
，则
的最小值为（ ）
| A．3 | B． | C．2 | D． |
若
，则满足不等式
的x的范围是（ ）
A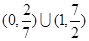． | B． |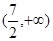
C． | D． |
函数
的值域为（ ）
A． | B． | C． | D． |
若a>0，a≠1，且m>0，n>0，则下列各式中正确的是 ( )
| A．logam•logan=loga(m+n) | B．am•an=am•n |
C． | D． |