Question

已知f(x)＝3－2|x|，g(x)＝x²－2x，构造函数F(x)，定义如下：f(x)≥g(x)时，F(x)＝g(x)；当f(x)＜g(x)时，F(x)＝f(x)，那么F(x)

[　　]

A．有最大值3，最小值－1

B．有最大值7－，无最小值

C．有最大值3，无最小值

D．无最大值，也无最小值

Answer 1

答案：B
解析：

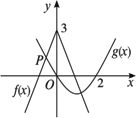
如图F(x)在点P处取最大值，由3＋2x＝x2－2x求得x＝2－7， 　　代入3－2|x|＝3＋2x＝7－，F(x)无最小值． 　　综合得F(x)最大值为7－，无最小值．