题目内容
已知f(x)=log3x+2,x∈[1,3],则函数F=[f(x)]2+f(x2)的最大值为
[ ]
A.13
B.16
C.18
D.![]()
答案:D
解析:
解析:
|
由f(x)=log3x+2的定义域为[1,3],则函数F=[f(x)]2+f(x2)的定义域为 故F(x)=(log3x+2)2+log3x2+2=(log3x)2+6log3x+6, 即F(u)=u2+6u+6,u∈[0, |

练习册系列答案
相关题目
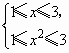 即1≤x≤
即1≤x≤ |sinx|.
|sinx|.