题目内容
已知点D(0，－2)，过点D作抛物线C1：x2＝2py(p＞0)的切线l，切点A在第二象限，如下图．
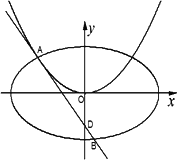
(Ⅰ)求切点A的纵坐标；
(Ⅱ)若离心率为
的椭圆恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若k1＋2k2＝4k，求椭圆方程．
答案：
解析：
解析：
|
解：(Ⅰ)设切点 由切线 (Ⅱ)由(Ⅰ)得 设 由 将 椭圆方程为
|
，且
，
的斜率为
，得
的方程为
，又点
在
上，
，即点
的纵坐标
．
，切线斜率
，
，切线方程为
，由
，得
，所以椭圆方程为
，且过
，
，
代入得：
，所以
，
．
练习册系列答案
应用题作业本系列答案
相关题目
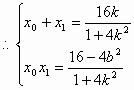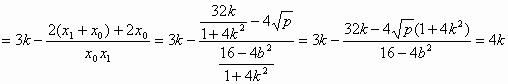
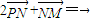的椭圆
恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若2k1＋k2＝3k，求抛物线C1和椭圆C2的方程．
与双曲线C恒有两个不同的交点A和B，且
＞2(其中O为原点)，求k的取值范围；
,0),在（2）的条件下，求M到直线l的距离d的取值范围.
．