题目内容
已知中心在坐标原点的双曲线C的右焦点为(2,0),右顶点为(3,0).(1)求双曲线C的方程;
(2)求若直线l:y=kx+![]() 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且![]() >2(其中O为原点),求k的取值范围;
>2(其中O为原点),求k的取值范围;
(3)已知点M(![]() ,0),在(2)的条件下,求M到直线l的距离d的取值范围.
,0),在(2)的条件下,求M到直线l的距离d的取值范围.
思路分析:对于(1),可先设双曲线C的方程,再由题意求出a,b的值;对于(2),为直线与双曲线的交点问题,联立方程,解方程组即可;(3)为点到直线的距离问题,代入点到直线的距离公式求解即可.
解:(1)设双曲线方程为![]() =1(a>0,b>0),由已知得a=
=1(a>0,b>0),由已知得a=![]() ,c=2.
,c=2.
∴b=1.故所求双曲线的方程为![]() =1,即
=1,即![]() =1.
=1.
(2)将y=kx+![]() 代入
代入![]() =1,可得(1-3k2)x2-
=1,可得(1-3k2)x2-![]() -9=0.
-9=0.
由直线l:y=kx+![]() 与双曲线C恒有两个不同的交点,得
与双曲线C恒有两个不同的交点,得

故k2≠![]() 且k2<1. ①
且k2<1. ①
设A(x1,y1),B(x2,y2),则x1+x2=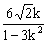 ,x1x2=
,x1x2=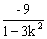 .
.
由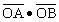 >2,得x1x2+y1y2>2.
>2,得x1x2+y1y2>2.
而x1x2+y1y2=x1x2+(kx1+![]() )(kx2+
)(kx2+![]() )=(k2+1)x1x2+
)=(k2+1)x1x2+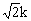 (x1+x2)+2=(k2+1)·
(x1+x2)+2=(k2+1)·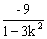 +
+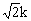 ·
·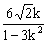 +2=
+2=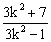 ,
,
∴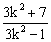 >2.
>2.
解此不等式,得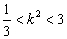 . ②
. ②
由①②,得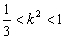 .故k的取值范围是(-1,
.故k的取值范围是(-1,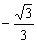 )∪(
)∪(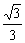 ,1).
,1).
(3)点M到直线l的距离为d=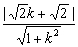 .
.
∴d2=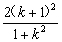 =
=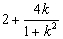 ,k∈(-1,
,k∈(-1,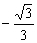 )∪(
)∪(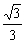 ,1)
,1)
设f(k)=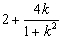 ,k∈(-1,
,k∈(-1,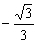 )∪(
)∪(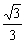 ,1),
,1),
则f′(k)=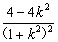 . ∵
. ∵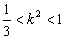 ,∴f′(k)>0.
,∴f′(k)>0.
∴f(k)在区间(-1,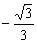 )∪(
)∪(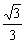 ,1)上均为增函数.
,1)上均为增函数.
当k∈(-1,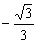 )时,f(-1)<f(k)<f(
)时,f(-1)<f(k)<f(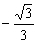 ),
),
即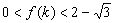 .此时
.此时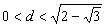 ;
;
当k∈(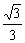 ,1)时,f(
,1)时,f(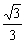 )<f(k)<f(1),
)<f(k)<f(1),
即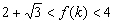 .此时
.此时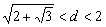 .
.
综上所得M到直线l的距离d的取值范围是(0,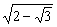 )∪(
)∪(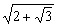 ,2).
,2).

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 的椭圆
的椭圆 经过点
经过点 ,且点
,且点 为其右焦点。
为其右焦点。 的直线
的直线 ,使得直线
,使得直线