题目内容
已知某圆的极坐标方程是 ,求:
,求:
(1)求圆的普通方程和一个参数方程;
(2)圆上所有点 中
中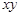 的最大值和最小值.
的最大值和最小值.
(1)即圆的普通方程为: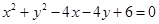 。 参数方程为:
。 参数方程为: 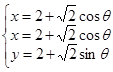 (
( 为参数) ;(2)最大值为:9,最小值为:1.
为参数) ;(2)最大值为:9,最小值为:1.
解析试题分析:(1)圆的普通方程与圆的极坐标方程之间的转换关系在于圆上一点 与极径
与极径 ,极角
,极角 间的关系:
间的关系: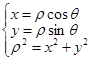 ,圆的普通方程与圆的参数方程的关系也在于此,即圆上一点
,圆的普通方程与圆的参数方程的关系也在于此,即圆上一点 与圆半径
与圆半径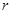 ,圆上点与圆心
,圆上点与圆心 连线与
连线与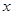 轴正向夹角
轴正向夹角 的关系:
的关系: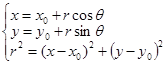 ;(2)利用圆的参数方程,将
;(2)利用圆的参数方程,将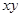 转化为关于
转化为关于 的三角函数关系求最值,注意这里处理要注意用换元法(不同于一般三角函数处理方法,即转化为
的三角函数关系求最值,注意这里处理要注意用换元法(不同于一般三角函数处理方法,即转化为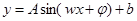 的形式),得到三角函数与二次函数的复合函数.
的形式),得到三角函数与二次函数的复合函数.
试题解析:
由圆上一点 与极径
与极径 ,极角
,极角 间的关系:
间的关系: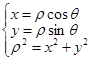 ,
, ,
,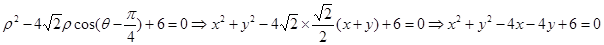
即圆的普通方程为: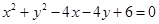 。 2分
。 2分
可得圆心坐标为 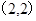 ,半径
,半径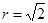
所以其参数方程为: 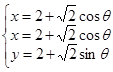 (
( 为参数) 。 4分
为参数) 。 4分
由圆上一点与圆的参数方程的关系得: 5分
5分
令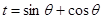 ,
,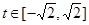 , 则
, 则 .
.
所以 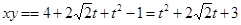 6分
6分
当 时,最小值是1; 8分
时,最小值是1; 8分
当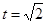 时,最大值是9. 10分
时,最大值是9. 10分
考点:(1)圆的极坐标方程与圆的参数方程;(2)参数方程求最值应用。

练习册系列答案
相关题目
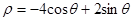 ②
②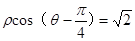
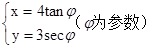 ④
④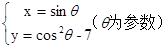
 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线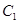 的方程为
的方程为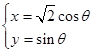 (
( 为参数),曲线
为参数),曲线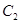 的极坐标方程为
的极坐标方程为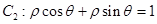 ,若曲线
,若曲线 、
、 两点.
两点.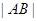 的值;
的值; 到
到 的参数方程为
的参数方程为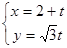 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为
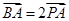 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.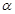 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程; 距离的最大值.
距离的最大值. 的参数方程是
的参数方程是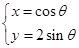 (
(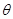 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,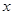 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是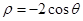 .
.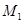 、
、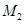 的极坐标分别是
的极坐标分别是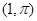 、
、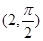 ,直线
,直线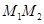 与曲线
与曲线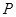 、
、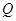 两点,射线
两点,射线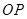 与曲线
与曲线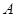 ,射线
,射线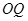 与曲线
与曲线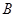 ,求
,求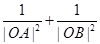 的值.
的值.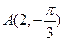 到直线
到直线 的距离为 .
的距离为 .