题目内容
计算:(1)-5log94+log3| 32 |
| 9 |
| 1 |
| 64 |
| 2 |
| 3 |
(2)tan2250tan6600-4sin2100cos3300.
分析:(1)利用对数的换底公式、负指数幂的公式及对数的运算性质化简可得值;
(2)利用诱导公式及特殊角的三角函数值化简可得值.
(2)利用诱导公式及特殊角的三角函数值化简可得值.
解答:解:(1)原式=-5log32+(log325-log332)-3-64
=-5log32+5log32-2log33-3-16=-2-3-16=-21;
(2)原式=tan(180°+45°)tan(720°-60°)-4sin(180°+30°)cos(360°-30°)
=tan45°(-tan60°)-4(-sin30°)cos30°
=-
-4(-
)×
=0.
| 2 |
| 3 |
=-5log32+5log32-2log33-3-16=-2-3-16=-21;
(2)原式=tan(180°+45°)tan(720°-60°)-4sin(180°+30°)cos(360°-30°)
=tan45°(-tan60°)-4(-sin30°)cos30°
=-
| 3 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查学生灵活运用对数的运算性质及诱导公式进行化简求值,学生做题时应灵活变换角的度数,牢记特殊角的三角函数值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
根据给出的算法框图,计算f(-1)+f(2)=( )
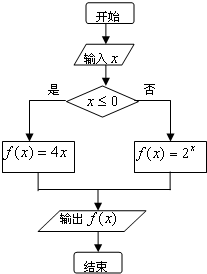

| A、0 | B、1 | C、2 | D、4 |
