题目内容
已知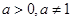 ,数列
,数列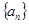 是首项为
是首项为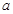 ,公比也为
,公比也为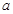 的等比数列,令
的等比数列,令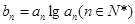
(Ⅰ)求数列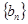 的前
的前 项和
项和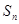 ;
;
(Ⅱ)当数列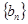 中的每一项总小于它后面的项时,求
中的每一项总小于它后面的项时,求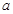 的取值范围.
的取值范围.
【答案】
(1)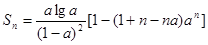 ;(2)
;(2)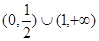 .
.
【解析】
试题分析:本题考查数列的通项公式和数列求和问题,考查学生的计算能力和分析问题解决问题的能力,考查分类讨论思想和转化思想.第一问,利用等比数列的通项公式先写出数列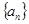 的通项公式,利用对数的性质得到
的通项公式,利用对数的性质得到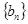 的通项公式,从而列出
的通项公式,从而列出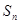 ,它符合错位相减法,利用错位相减法求和;第二问,有题意得
,它符合错位相减法,利用错位相减法求和;第二问,有题意得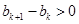 ,讨论
,讨论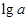 的正负,转化为恒成立问题,求出
的正负,转化为恒成立问题,求出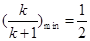 .
.
试题解析:(Ⅰ)由题意知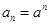 ,
,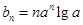 .
.
∴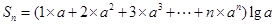 .
.
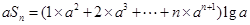 .
.
以上两式相减得
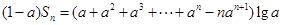
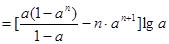 .
.
∵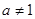 ,∴
,∴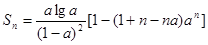 .
.
(Ⅱ)由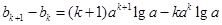
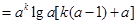 .
.
由题意知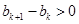 ,而
,而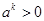 ,
,
∴ . ①
. ①
(1)若 ,则
,则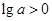 ,
,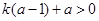 ,故
,故 时,不等式①成立;
时,不等式①成立;
(2)若 ,则
,则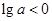 ,
,
不等式①成立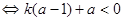
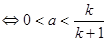 恒成立
恒成立
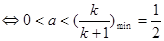 .
.
综合(1)、(2)得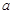 的取值范围为
的取值范围为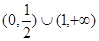 .
.
考点:1.等比数列的通项公式;2.等比数列的前n项和公式;3.错位相减法;4.恒成立问题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
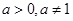 ,数列
,数列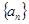 是首项为
是首项为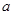 ,公比也为
,公比也为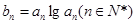
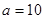 ,求数列
,求数列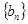 的前
的前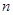 项和
项和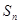 ;
;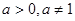 ,数列
,数列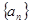 是首项为a,公比也为a的等比数列,令
是首项为a,公比也为a的等比数列,令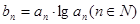 ,求数列
,求数列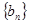 的前
的前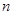 项和
项和 。
。