题目内容
 注意:在以下(1)(2)两题中任选一题.如果两题都做,按(1)给分.
注意:在以下(1)(2)两题中任选一题.如果两题都做,按(1)给分.(1)(坐标系与参数方程选做题)极坐标系中,A(2,
| π |
| 6 |
| 5π |
| 6 |
| 19 |
| 19 |
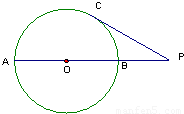
(2)(几何证明选讲选做题)如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2.则⊙O的半径等于
3
3
.分析:(1)极坐标化为直角坐标的公式:x=ρcosθ,y=ρsinθ.由此将点A、B都化成直角坐标的形式,再用两个间的距离公式AB=
,从而求出A、B两点的距离.
(2)根据题意,可得PC是PA和PB的比例中项,再将数据PC=4,PB=2代入,可得⊙O的直径的长度,从而得出⊙O的半径长.
| (x1-x2) 2+(y1-y2) 2 |
(2)根据题意,可得PC是PA和PB的比例中项,再将数据PC=4,PB=2代入,可得⊙O的直径的长度,从而得出⊙O的半径长.
解答:解:(1)∵极坐标系中,A的坐标为(2,
)
∴直角坐标系中,设A的坐标为(x1,y1)可得
x1=2cos
=
,y1=2sin
=1
∴A点的直角坐标为(
,1)
同理可得B点的直角坐标为(-
,
)
因此A、B两点的距离为AB=
=
(2)由切割线定理,得:PC2=PA•PB
设圆的半径为R,结合PC=4,PB=2得:42=2(2+2R)
∴R=3,即⊙O的半径等于3
故答案为:
、3
| π |
| 6 |
∴直角坐标系中,设A的坐标为(x1,y1)可得
x1=2cos
| π |
| 6 |
| 3 |
| π |
| 6 |
∴A点的直角坐标为(
| 3 |
同理可得B点的直角坐标为(-
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
因此A、B两点的距离为AB=
(-
|
| 19 |
(2)由切割线定理,得:PC2=PA•PB
设圆的半径为R,结合PC=4,PB=2得:42=2(2+2R)
∴R=3,即⊙O的半径等于3
故答案为:
| 19 |
点评:本题第一问考查了简单曲线的极坐标方程,第二问考查了与圆有关的比例线段,都属于基础题.注意解第一问题中,化极坐标为直角坐标,是解决此类问题的常用思路.

练习册系列答案
相关题目
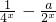 (a∈R)
(a∈R)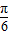 ),B(3,
),B(3,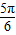 ),则A、B两点的距离是: .
),则A、B两点的距离是: .