题目内容
在锐角三角形中,若角A、B、C所对的边分别为a、b、c,若B=2A,则
的取值范围是
<
<
<
<
.
| a |
| b |
| ||
| 3 |
| a |
| b |
| ||
| 2 |
| ||
| 3 |
| a |
| b |
| ||
| 2 |
分析:先确定A的范围,再确定
<cosA<
.利用正弦定理,化简
,即可得到结论.
| ||
| 2 |
| ||
| 2 |
| a |
| b |
解答:解:∵三角形是锐角三角形,∴C<
∴π-A-B<
∵B=2A,∴A>
∵B=2A<
,∴A<
∴
<A<
∴
<cosA<
∵
=
=
=
∴
<
<
故答案为:
<
<
| π |
| 2 |
∴π-A-B<
| π |
| 2 |
∵B=2A,∴A>
| π |
| 6 |
∵B=2A<
| π |
| 2 |
| π |
| 4 |
∴
| π |
| 6 |
| π |
| 4 |
∴
| ||
| 2 |
| ||
| 2 |
∵
| a |
| b |
| sinA |
| sinB |
| sinA |
| sin2A |
| 1 |
| 2cosA |
∴
| ||
| 3 |
| a |
| b |
| ||
| 2 |
故答案为:
| ||
| 3 |
| a |
| b |
| ||
| 2 |
点评:本题考查正弦定理的运用,考查学生的计算能力,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
. 的大小;
的大小; ,且
,且 ,求
,求 的值.
的值. 的取值范围是________.
的取值范围是________.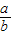 的取值范围是 .
的取值范围是 .