Question

(本小题满分12分)直三棱柱ABC -A₁B₁C₁中，AB=5，AC=4，BC=3，AA₁=4，点D在AB上．

（Ⅰ）求证：AC⊥B₁C；

（Ⅱ）若D是AB中点，求证：AC₁∥平面B₁CD；

（Ⅲ）当时，求二面角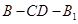的余弦值．

 

 

 

Answer 1

【答案】

18.（Ⅰ）证明：在△ABC中，因为  AB=5，AC=4，BC=3，

所以 AC²+ BC²= AB²，  所以  AC⊥BC．                      

因为 直三棱柱ABC-A₁B₁C₁，所以 C C₁⊥AC．                  

因为 BC∩AC =C，所以 AC⊥平面B B₁C₁C．     

所以 AC⊥B₁C．          …………4分

（Ⅱ）证明：连结BC₁，交B₁C于E，连接DE．

因为 直三棱柱ABC-A₁B₁C₁，D是AB中点，所以 侧面B B₁C₁C为矩形，DE为△ABC₁的中位线，

所以 DE// AC₁．因为 DE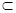平面B₁CD， AC₁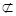平面B₁CD，所以 AC₁∥平面B₁CD．........8分

 

 

（Ⅲ）解：由（Ⅰ）知AC⊥BC，如图，以C为原点建立空间直角坐标系C-xyz．则B (3, 0, 0)，A (0, 4, 0)，A₁ (0, 4, 4)，B₁ (3, 0, 4)．

设D (a, b, 0)（，），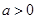

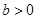因为 点D在线段AB上，且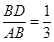，即．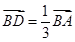

所以，，，, ,．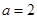

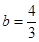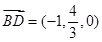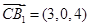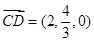平面BCD的法向量为． 设平面B₁ CD的法向量为，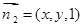

由 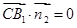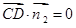，， 得 ，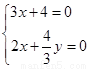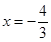

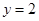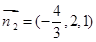所以 ，，.所以  ．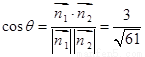

所以二面角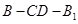的余弦值为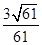． ……………12分

【解析】略