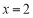题目内容
已知函数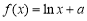 ,
, ,
, .
.
(1)若 ,设函数
,设函数 ,求
,求 的极大值;
的极大值;
(2)设函数 ,讨论
,讨论 的单调性.
的单调性.
(1)极大值 ;(2)当
;(2)当 时,
时, 的增区间为
的增区间为 ,
,
当 时,
时,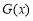 的增区间为
的增区间为 ,减区间为
,减区间为 .
.
【解析】
试题分析:(1)函数求极值分三步:①对函数求导;②令导函数为零求根,判断根是否为极值点;③求出极值;(2)先求导函数,然后利用导数求单调性,在其中要注意对a的分类讨论.
试题解析:(1)当 时,
时, ,定义域为
,定义域为 ,
,
则 . 2分
. 2分
令 ,列表: 4分
,列表: 4分
|
| 1 |
|
| + | 0 | — |
| ↗ | 极大值 | ↘ |
当 时,
时, 取得极大值
取得极大值 . 7分
. 7分
(2) ,∴
,∴ . 9分
. 9分
若 ,
, ,
, 在
在 上递增; 11分
上递增; 11分
若 ,当
,当 时,
时, ,
, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减. 14分
单调递减. 14分
∴当 时,
时, 的增区间为
的增区间为 ,
,
当 时,
时,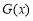 的增区间为
的增区间为 ,减区间为
,减区间为 . 16分
. 16分
考点:(1`)导数求单调性与极值;(2)分类讨论数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目