题目内容
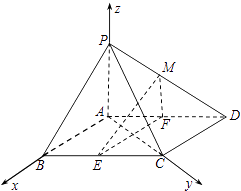
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. 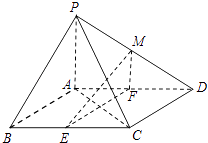
(1)求证:EF⊥平面PAC;
(2)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.
【答案】
(1)证明:∵在平行四边形ABCD中,∠BCD=135°,∴∠ABC=45°,
∵AB=AC,∴AB⊥AC.
∵E,F分别为BC,AD的中点,∴EF∥AB,
∴EF⊥AC.
∵侧面PAB⊥底面ABCD,且∠BAP=90°,
∴PA⊥底面ABCD.
又EF底面ABCD,
∴PA⊥EF.
又∵PA∩AC=A,PA平面PAC,AC平面PAC,
∴EF⊥平面PAC.
(2)解:∵PA⊥底面ABCD,AB⊥AC,∴AP,AB,AC两两垂直,
以A为原点,分别以AB,AC,AP为x轴、y轴和z轴建立空间直角坐标系如图:
则A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,2),D(﹣2,2,0),E(1,1,0),
∴ ![]() =(2,0,﹣2),
=(2,0,﹣2), ![]() =(﹣2,2,﹣2),
=(﹣2,2,﹣2), ![]() ,
, ![]() =(1,1,﹣2).
=(1,1,﹣2).
设 ![]() =λ(0≤λ≤1),则
=λ(0≤λ≤1),则 ![]() =(﹣2λ,2λ,﹣2λ),
=(﹣2λ,2λ,﹣2λ),
∴ ![]() =
= ![]() -
- ![]() =(1+2λ,1﹣2λ,2λ﹣2),
=(1+2λ,1﹣2λ,2λ﹣2),
显然平面ABCD的一个法向量为 ![]() =(0,0,1).
=(0,0,1).
设平面PBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 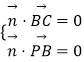 ,即
,即 ![]()
令x=1,得 ![]() =(1,1,1).
=(1,1,1).
∴cos< ![]() ,
, ![]() >=
>= 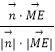 =
= ![]() ,cos<
,cos< ![]() >=
>= 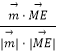 =
= ![]() .
.
∵直线ME与平面PBC所成的角和此直线与平面ABCD所成的角相等,
∴| ![]() |=|
|=| ![]() |,即
|,即 ![]() ,
,
解得 ![]() ,或
,或 ![]() (舍).
(舍).
∴ ![]()
![]() .
.
【解析】(1)由平行四边形的性质可得AB⊥AC,即EF⊥AC,由面面垂直的性质得出PA⊥平面ABCD,故PA⊥EF,故EF⊥平面PAC;(2)以A为原点建立空间直角坐标系,设 ![]() =λ(0≤λ≤1),求出平面PBC,平面ABCD的法向量
=λ(0≤λ≤1),求出平面PBC,平面ABCD的法向量 ![]() 及
及 ![]() 的坐标,根据线面角相等列方程解出λ.
的坐标,根据线面角相等列方程解出λ.