题目内容
6个大小相同的小球分别标有数字1,1,1,2,2,2,把它们放在一个盒子里,从中任意摸出两个小球,它们所标有的数字分别为x,y,记ξ=x+y.(1)求随机变量ξ分布列及数学期望.
(2)设“函数f (x)=x2-ξx-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率.
分析:(1)由题知随机变量ξ的可能取值为2,3,4.结合变量对应的事件,求每一个事件的概率,当变量是2时,从盒子中摸出两个小球的基本事件总数为C62,摸出的小球所标的数字为1,1,共有C32种.得到概率,以此类推,写出分布列和期望.
(2)首先整理函数f(x)=x2-ξx-1在(2,3)上有且只有一个零点时,要满足的条件,根据实根存在性定理得到f(2)•f(3)<0即(3-2ξ)(8-3ξ)<0,求出变量的范围,得到对应的ξ的值,根据第一问做出结果,得到概率.
(2)首先整理函数f(x)=x2-ξx-1在(2,3)上有且只有一个零点时,要满足的条件,根据实根存在性定理得到f(2)•f(3)<0即(3-2ξ)(8-3ξ)<0,求出变量的范围,得到对应的ξ的值,根据第一问做出结果,得到概率.
解答:解:(1)由题知随机变量ξ的可能取值为2,3,4.
从盒子中摸出两个小球的基本事件总数为C62=15.
当ξ=2时,摸出的小球所标的数字为1,1,共有C32种.
∴P(ξ=2)=
.
当ξ=3时,摸出的小球所标的数字为1,2,共有C31•C31种.
∴P(ξ=3)=
.
当ξ=4时,摸出的小球所标的数字为2,2,共有C32种.
∴P(ξ=4)=
.
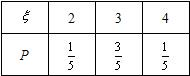
∴ξ的分布列为
Eξ=2×
+3×
+4×
=3.
(2)∵函数f(x)=x2-ξx-1在(2,3)上有且只有一个零点.
f(2)•f(3)<0即(3-2ξ)(8-3ξ)<0
∴
<ξ<
且ξ=2,3,4
∴ξ=2.
∴P(A)=P(ξ=2)=
.
从盒子中摸出两个小球的基本事件总数为C62=15.
当ξ=2时,摸出的小球所标的数字为1,1,共有C32种.
∴P(ξ=2)=
| 1 |
| 5 |
当ξ=3时,摸出的小球所标的数字为1,2,共有C31•C31种.
∴P(ξ=3)=
| 3 |
| 5 |
当ξ=4时,摸出的小球所标的数字为2,2,共有C32种.
∴P(ξ=4)=
| 1 |
| 5 |
∴ξ的分布列为

Eξ=2×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
(2)∵函数f(x)=x2-ξx-1在(2,3)上有且只有一个零点.
f(2)•f(3)<0即(3-2ξ)(8-3ξ)<0
∴
| 3 |
| 2 |
| 8 |
| 3 |
∴ξ=2.
∴P(A)=P(ξ=2)=
| 1 |
| 5 |
点评:本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,考查函数零点的存在性定理,考查用概率知识解决数学问题,是一个综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求
,求 ,求
,求 ,求红球的个数;
,求红球的个数; ,求红球的个数.
,求红球的个数.