题目内容
已知定义在R上的函数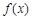 的图象关于点(-
的图象关于点(-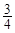 ,0)对称,且满足
,0)对称,且满足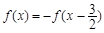 ,
,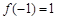 ,
,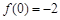 ,则
,则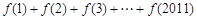 的值是
的值是
| A.2 | B.1 | C.-1 | D.-2 |
B
解析考点:抽象函数及其应用;函数的值.
分析:由函数图象关于点(- 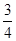 ,0)对称,知f(x)="-f(-x-"
,0)对称,知f(x)="-f(-x-"  ),由f(x)="-f(x-"
),由f(x)="-f(x-"  )可得f(x)=f(x-3),从而f(x)=f(x+3),f(x)是最小正周期为3的周期函数;再由f(-x-
)可得f(x)=f(x-3),从而f(x)=f(x+3),f(x)是最小正周期为3的周期函数;再由f(-x-  )="f(x+"
)="f(x+"  ),可得故f(x)是偶函数,从而结合条件可求得f(1),f(2),f(3)的值.
),可得故f(x)是偶函数,从而结合条件可求得f(1),f(2),f(3)的值.
解:∵函数图象关于点(-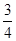 ,0)对称,
,0)对称,
∴f(x)=-f(-x- ),①
),①
∵f(x)=-f(x- ),即f(x-
),即f(x- )=-f(x),
)=-f(x),
∴f[(x- )-
)- ]=-f(x-
]=-f(x- )=f(x),即f(x-3)=f(x)=f[(x-3)+3],
)=f(x),即f(x-3)=f(x)=f[(x-3)+3],
∴f(x+3)=f(x);
∴f(x)是最小正周期为3的周期函数;
又f(-x- )=f(x+
)=f(x+ ),故f(x)是偶函数.
),故f(x)是偶函数.
∴f(-1)=f(2)=1,f(1)=f(-1)=1,f(3)=f(0)=-2,
∴f(1)+f(2)+f(3)=0,又f(x)是最小正周期为3的周期函数,
∴f(1)+f(2)+f(3)+…+f(2011)
=f(2011)=f(3×670+1)=f(1)=1.
故选B.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |