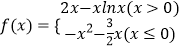Question

【题目】对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″是f′（x）的导数，若方程f″（x）=0有实数解x0 ， 则称点（x0 ， f（x0））为函数y=f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．请你根据这一发现，求：函数 对称中心为 ．

Answer 1

【答案】（ ，1）
【解析】解：依题意，得：f′（x）=x2﹣x+3，∴f″（x）=2x﹣1． 由f″（x）=0，即2x﹣1=0．
∴x= ，
又 f（ ）=1，
∴函数 对称中心为（ ，1）
故答案为：（ ，1）
先求f′（x）得解析式，再求f″（x），由f″（x）=0 求得拐点的横坐标，代入函数解析式求拐点的纵坐标．