题目内容
函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0);
(2)求f(x);
(3)不等式f(x)>ax-5当0<x<2时恒成立,求a的取值范围.
(1)求f(0);
(2)求f(x);
(3)不等式f(x)>ax-5当0<x<2时恒成立,求a的取值范围.
(1)-2(2) f(x)=x2+x-2(3) a<1+2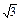
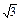
(1)令x=1,y=0,
得f(1+0)-f(0)=(1+2×0+1)·1=2,
∴f(0)=f(1)-2=-2.
(2)令y=0,f(x+0)-f(0)=(x+2×0+1)·x=x2+x,
∴f(x)=x2+x-2.
(3)f(x)>ax-5化为x2+x-2>ax-5,
ax<x2+x+3,∵x∈(0,2),
∴a<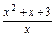 =1+x+
=1+x+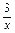 .
.
当x∈(0,2)时,1+x+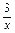 ≥1+2
≥1+2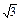 ,当且仅当x=
,当且仅当x=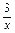 ,即x=
,即x=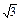 时取等号,由
时取等号,由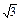 ∈(0,2),得
∈(0,2),得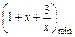 =1+2
=1+2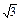 .
.
∴a<1+2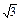 .
.
得f(1+0)-f(0)=(1+2×0+1)·1=2,
∴f(0)=f(1)-2=-2.
(2)令y=0,f(x+0)-f(0)=(x+2×0+1)·x=x2+x,
∴f(x)=x2+x-2.
(3)f(x)>ax-5化为x2+x-2>ax-5,
ax<x2+x+3,∵x∈(0,2),
∴a<
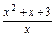 =1+x+
=1+x+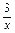 .
.当x∈(0,2)时,1+x+
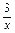 ≥1+2
≥1+2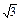 ,当且仅当x=
,当且仅当x=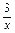 ,即x=
,即x=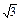 时取等号,由
时取等号,由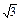 ∈(0,2),得
∈(0,2),得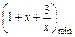 =1+2
=1+2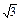 .
. ∴a<1+2
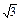 .
.
练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
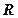 上定义运算:
上定义运算: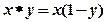 ,若不等式
,若不等式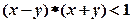 对一切实数
对一切实数 恒成立,则实数
恒成立,则实数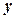 的取值范围是____________
的取值范围是____________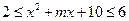 有且只有一个解,求实数
有且只有一个解,求实数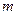 的值。
的值。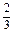 >0;(2)9x2-6x+1≥0.
>0;(2)9x2-6x+1≥0.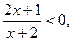 判断方程
判断方程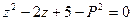 有
有 的解集是
的解集是 ,则
,则 的值是( )
的值是( )

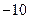


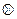 为:x
为:x
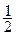 <a<
<a<