题目内容
已知x2 = a2 + b2，y2 = c2 + d2，且所有字母均为正，求证：xy≥ac + bd
同解析。
∵a, b, c, d, x, y都是正数 ∴要证：xy≥ac + bd
只需证：(xy)2≥(ac + bd)2 即：(a2 + b2)(c2 + d2)≥a2c2 + b2d2 + 2abcd
展开得：a2c2 + b2d2 + a2d2 + b2c2≥a2c2 + b2d2 + 2abcd
即：a2d2 + b2c2≥2abcd 由基本不等式，显然成立
∴xy≥ac + bd
只需证：(xy)2≥(ac + bd)2 即：(a2 + b2)(c2 + d2)≥a2c2 + b2d2 + 2abcd
展开得：a2c2 + b2d2 + a2d2 + b2c2≥a2c2 + b2d2 + 2abcd
即：a2d2 + b2c2≥2abcd 由基本不等式，显然成立
∴xy≥ac + bd
练习册系列答案
名校课堂系列答案
相关题目
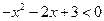的解集.
有两个负数根,则实数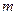
的范围是( )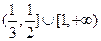
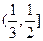
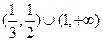
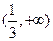
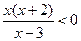的解集是为 .
满足
，则
的最大值
是
，且
，那么
的取值范围是 ．