题目内容
定义在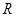 上的偶函数
上的偶函数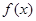 在
在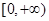 上单调递减,且
上单调递减,且 ,则满足
,则满足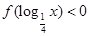 的集合为________.
的集合为________.
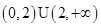
解析试题分析:因为定义在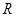 上的偶函数
上的偶函数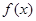 在
在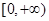 上单调递减,所以在
上单调递减,所以在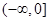 上单调递增.又
上单调递增.又 ,所以
,所以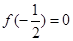 .所以由
.所以由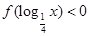 可得
可得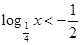 ,或
,或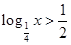 ,
,
解得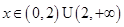 .
.
考点:本小题主要考查函数的奇偶性、函数的单调性的应用和对数不等式的解法.
点评:解不等式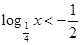 ,或
,或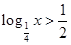 时,不要忘记
时,不要忘记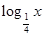 本身要求
本身要求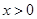 ,
,

练习册系列答案
相关题目
题目内容
定义在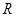 上的偶函数
上的偶函数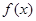 在
在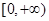 上单调递减,且
上单调递减,且 ,则满足
,则满足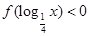 的集合为________.
的集合为________.
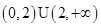
解析试题分析:因为定义在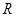 上的偶函数
上的偶函数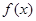 在
在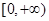 上单调递减,所以在
上单调递减,所以在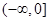 上单调递增.又
上单调递增.又 ,所以
,所以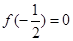 .所以由
.所以由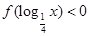 可得
可得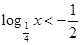 ,或
,或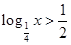 ,
,
解得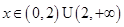 .
.
考点:本小题主要考查函数的奇偶性、函数的单调性的应用和对数不等式的解法.
点评:解不等式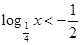 ,或
,或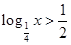 时,不要忘记
时,不要忘记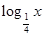 本身要求
本身要求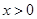 ,
,
