题目内容
【选修4-4:坐标系与参数方程】
在直角坐标系xoy中,直线l的参数方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2
sinθ.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A、B,若点P的坐标为(3,
),求|PA|+|PB|.
在直角坐标系xoy中,直线l的参数方程为
|
| 5 |
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A、B,若点P的坐标为(3,
| 5 |
分析:(Ⅰ)把给出的等式的两边同时乘以ρ,然后代入ρ2=x2+y2,y=ρsinθ得答案;
(Ⅱ)把直线的参数方程代入圆的直角坐标方程,化为关于t的一元二次方程后由参数t的几何意义得答案.
(Ⅱ)把直线的参数方程代入圆的直角坐标方程,化为关于t的一元二次方程后由参数t的几何意义得答案.
解答:解:(Ⅰ)由ρ=2
sinθ,得ρ2=2
ρsinθ,
即x2+y2-2
y=0,x2+(y-
)2=5;
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得(3-
t)2+(
t)2=5,
即t2-3
t+4=0,
由于△=(3
)2-4×4=2>0,
故可设t1,t2是上述方程的两根,
∴
,
又直线l过点P(3,
),故由上式及t的几何意义得:
|PA|+|PB|=|t1|+|t2|=t1+t2=3
.
| 5 |
| 5 |
即x2+y2-2
| 5 |
| 5 |
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,得(3-
| ||
| 2 |
| ||
| 2 |
即t2-3
| 2 |
由于△=(3
| 2 |
故可设t1,t2是上述方程的两根,
∴
|
又直线l过点P(3,
| 5 |
|PA|+|PB|=|t1|+|t2|=t1+t2=3
| 2 |
点评:本题主要考查直线的参数方程、圆的极坐标方程、直线与圆的位置关系等基础知识,考查运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的参数方程为
的参数方程为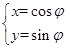 (
(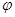 为参数),以坐标原点
为参数),以坐标原点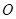 为极点,
为极点,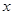 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为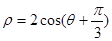 .
. 为极点,
为极点,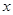 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点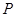 的直角坐标为
的直角坐标为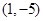 ,点
,点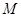 的极坐标为
的极坐标为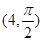 ,若直线
,若直线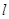 过点
过点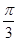 ,圆
,圆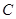 以
以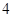 为半径。
为半径。