题目内容
【选修4-4:坐标系与参数方程】
(1)求点M(2,
)到直线ρ=
上点A的距离的最小值.
(2)求曲线C:
(θ为参数)关于直线y=1对称的曲线的参数方程.
(1)求点M(2,
| π |
| 3 |
| ||
| sinθ+cosθ |
(2)求曲线C:
|
分析:(1)点M(2,
)化为直角坐标M(2cos
,2sin
)即M(1,
).直线ρ=
即ρsinθ+ρcosθ=
,化为直角坐标方程x+y-
=0.则点M(1,
)到直线上的点A的距离的最小值为点M到直线的距离.
(2)设曲线C:
(θ为参数)关于直线y=1对称的曲线上的点为P(x,y),则点P关于直线y=1的对称点P′(x,2-y),此点在曲线C上,可得
,即可.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| ||
| sinθ+cosθ |
| 3 |
| 3 |
| 3 |
(2)设曲线C:
|
|
解答:解:(1)点M(2,
)化为直角坐标M(2cos
,2sin
)即M(1,
).
直线ρ=
即ρsinθ+ρcosθ=
,化为直角坐标方程x+y-
=0.
则点M(1,
)到直线上的点A的距离的最小值为d=
=
.
∴点M(2,
)到直线ρ=
上点A的距离的最小值是
.
(2)设曲线C:
(θ为参数)关于直线y=1对称的曲线上的点为P(x,y),
则点P关于直线y=1的对称点P′(x,2-y),此点在曲线C上,
∴
,化为
即为所求曲线C关于直线y=1对称的曲线的参数方程.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
直线ρ=
| ||
| sinθ+cosθ |
| 3 |
| 3 |
则点M(1,
| 3 |
|1+
| ||||
|
| ||
| 2 |
∴点M(2,
| π |
| 3 |
| ||
| sinθ+cosθ |
| ||
| 2 |
(2)设曲线C:
|
则点P关于直线y=1的对称点P′(x,2-y),此点在曲线C上,
∴
|
|
点评:本题考查了把极坐标方程化为直角坐标方程、点到直线的距离公式、曲线关于直线的对称曲线、中点坐标公式等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
 的参数方程为
的参数方程为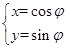 (
(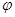 为参数),以坐标原点
为参数),以坐标原点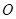 为极点,
为极点,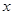 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为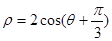 .
. 为极点,
为极点,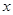 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点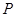 的直角坐标为
的直角坐标为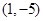 ,点
,点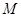 的极坐标为
的极坐标为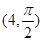 ,若直线
,若直线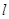 过点
过点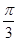 ,圆
,圆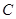 以
以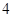 为半径。
为半径。