题目内容
设g(x)=2x+ ,x∈[
,x∈[ ,4].
,4].
(1)求g(x)的单调区间;(简单说明理由,不必严格证明)
(2)证明g(x)的最小值为g( );
);
(3)设已知函数f(x)(x∈[a,b]),定义:f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),f2(x)=max{f(t)|a≤t≤x}(x∈[a,b].其中,min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值.例如:f(x)=sinx,x∈[- ,
, ],则f1(x)=-1,x∈[-
],则f1(x)=-1,x∈[- ,
, ],f2(x)=sinx,x∈[-
],f2(x)=sinx,x∈[- ,
, ],设φ(x)=
],设φ(x)=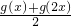 +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
解:(1)∵g(x)=2x+ 为奇函数.奇函数在对称区间单调性相同,
为奇函数.奇函数在对称区间单调性相同,
g(x)在x∈[ ,
, ]上递减,g(x)在x∈[
]上递减,g(x)在x∈[ ,4]上递增;
,4]上递增;
(2)用最值的定义证明:
g(x)在x∈[ ,
, ]上递减,
]上递减,
对任意x∈[ ,
, ],都有g(
],都有g( )≥g(x)≥g(
)≥g(x)≥g( );
);
g(x)在x∈[ ,4]上递增,对任意x∈[
,4]上递增,对任意x∈[ ,4],都有g(4)≥g(x)≥g(
,4],都有g(4)≥g(x)≥g( ).
).
综上,g(x)的最小值为g( ).
).
(3)先求定义域x∈[ ,2].
,2].
φ(x)=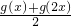 +
+ =
= ,
,
φ1(x)= ,)=
,)= ,
,
φ1(x)-φ2(x)= ,
,
由题设条件可得φ1(x)-φ2(x)的最小值为-5.25.
φ1(x)-φ2(x的最大值为0,
∴p≤-5.25,m≥0.
分析:(1)根据y=ax+ (a>0,b>0,x<0)单调性及奇函数在对称区间单调性相同即可求得g(x)的单调区间;
(a>0,b>0,x<0)单调性及奇函数在对称区间单调性相同即可求得g(x)的单调区间;
(2)利用(1)问g(x)的单调性可证明;
(3)先求定义域x∈[ ,2].由定义求出φ(x),φ1(x),φ2(x),进而表示出φ1(x)-φ2(x),由题设条件可得φ1(x)-φ2(x)的最小值及φ1(x)-φ2(x)的最大值问题即可解决.
,2].由定义求出φ(x),φ1(x),φ2(x),进而表示出φ1(x)-φ2(x),由题设条件可得φ1(x)-φ2(x)的最小值及φ1(x)-φ2(x)的最大值问题即可解决.
点评:本题考查函数的奇偶性、单调性及其应用,考查不等式恒成立问题,考查学生分析问题解决问题的能力.
 为奇函数.奇函数在对称区间单调性相同,
为奇函数.奇函数在对称区间单调性相同,g(x)在x∈[
 ,
, ]上递减,g(x)在x∈[
]上递减,g(x)在x∈[ ,4]上递增;
,4]上递增;(2)用最值的定义证明:
g(x)在x∈[
 ,
, ]上递减,
]上递减,对任意x∈[
 ,
, ],都有g(
],都有g( )≥g(x)≥g(
)≥g(x)≥g( );
);g(x)在x∈[
 ,4]上递增,对任意x∈[
,4]上递增,对任意x∈[ ,4],都有g(4)≥g(x)≥g(
,4],都有g(4)≥g(x)≥g( ).
).综上,g(x)的最小值为g(
 ).
).(3)先求定义域x∈[
 ,2].
,2].φ(x)=
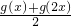 +
+ =
= ,
,φ1(x)=
 ,)=
,)= ,
,φ1(x)-φ2(x)=
 ,
,由题设条件可得φ1(x)-φ2(x)的最小值为-5.25.
φ1(x)-φ2(x的最大值为0,
∴p≤-5.25,m≥0.
分析:(1)根据y=ax+
 (a>0,b>0,x<0)单调性及奇函数在对称区间单调性相同即可求得g(x)的单调区间;
(a>0,b>0,x<0)单调性及奇函数在对称区间单调性相同即可求得g(x)的单调区间;(2)利用(1)问g(x)的单调性可证明;
(3)先求定义域x∈[
 ,2].由定义求出φ(x),φ1(x),φ2(x),进而表示出φ1(x)-φ2(x),由题设条件可得φ1(x)-φ2(x)的最小值及φ1(x)-φ2(x)的最大值问题即可解决.
,2].由定义求出φ(x),φ1(x),φ2(x),进而表示出φ1(x)-φ2(x),由题设条件可得φ1(x)-φ2(x)的最小值及φ1(x)-φ2(x)的最大值问题即可解决.点评:本题考查函数的奇偶性、单调性及其应用,考查不等式恒成立问题,考查学生分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目