题目内容
【题目】2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: (Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价 | 35岁以下人数 |
[2,4) | 2 |
[4,6) | 8 |
[6,8) | 12 |
[8,10) | 5 |
[10,12] | 3 |
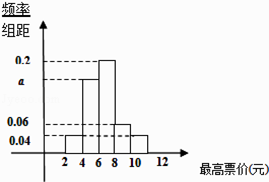
【答案】解:(Ⅰ)由题意得:0.04×2+a×2+0.2×2+0.06×2+0.04×2=1, 解得a=0.16
由频率分布直方图估计众数为7,
说明在被调查的50人中,能接受最高票价为7元的人数比能接受最高票价为其他值得人数多.
(Ⅱ)由题意知,
50名被调查者中:选择最高票价在[8,10)的人数为0.06×2×50=6人.
选择最高票价在[10,12]的人数为0.04×2×50=4人
故X的可能取值为0,1,2, ![]() ,
,![]() ,
,![]()
所以,X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
![]()
【解析】(Ⅰ)由题意得:0.04×2+a×2+0.2×2+0.06×2+0.04×2=1,由此能求出a;由频率分布直方图估计众数为7,说明在被调查的50人中,能接受最高票价为7元的人数比能接受最高票价为其他值得人数多.(Ⅱ)由题意知,X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列及数学期望.
【考点精析】本题主要考查了频率分布直方图和离散型随机变量及其分布列的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.

 备战中考寒假系列答案
备战中考寒假系列答案