题目内容
已知动点P与平面上两定点 连线的斜率的积为定值
连线的斜率的积为定值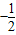 .
.(1)试求动点P的轨迹方程C;
(2)设直线l:y=kx+1与曲线C交于M.N两点,当
 时,求直线l的方程.
时,求直线l的方程.
【答案】分析:(Ⅰ)设出P的坐标,利用动点P与平面上两定点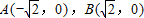 连线的斜率的积为定值
连线的斜率的积为定值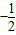 ,建立方程,化简可求动点P的轨迹方程C.
,建立方程,化简可求动点P的轨迹方程C.
(Ⅱ)直线l:y=kx+1与曲线C方程联立,利用韦达定理计算弦长,即可求得结论.
解答:解:(Ⅰ)设动点P的坐标是(x,y),由题意得:kPAkPB=
∴ ,化简,整理得
,化简,整理得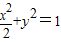
故P点的轨迹方程是 ,(x≠±
,(x≠± )
)
(Ⅱ)设直线l与曲线C的交点M(x1,y1),N(x2,y2),
由 得,(1+2k2)x2-4k2x+2k2-2=0
得,(1+2k2)x2-4k2x+2k2-2=0
∴x1+x2= ,x1 x2=
,x1 x2=
|AB|= ,
,
整理得,7k4-2k2-5=0,解得k2=1,或k2=- (舍)
(舍)
∴k=±1,经检验符合题意.
∴直线l的方程是y=±x+1,即:x-y+1=0或x+y-1=0
点评:本题考查轨迹方程的求解,考查直线与椭圆的位置关系,考查弦长公式的运用,考查学生的计算能力,属于中档题.
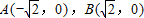 连线的斜率的积为定值
连线的斜率的积为定值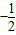 ,建立方程,化简可求动点P的轨迹方程C.
,建立方程,化简可求动点P的轨迹方程C.(Ⅱ)直线l:y=kx+1与曲线C方程联立,利用韦达定理计算弦长,即可求得结论.
解答:解:(Ⅰ)设动点P的坐标是(x,y),由题意得:kPAkPB=

∴
 ,化简,整理得
,化简,整理得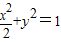
故P点的轨迹方程是
 ,(x≠±
,(x≠± )
)(Ⅱ)设直线l与曲线C的交点M(x1,y1),N(x2,y2),
由
 得,(1+2k2)x2-4k2x+2k2-2=0
得,(1+2k2)x2-4k2x+2k2-2=0∴x1+x2=
 ,x1 x2=
,x1 x2=
|AB|=
 ,
,整理得,7k4-2k2-5=0,解得k2=1,或k2=-
 (舍)
(舍)∴k=±1,经检验符合题意.
∴直线l的方程是y=±x+1,即:x-y+1=0或x+y-1=0
点评:本题考查轨迹方程的求解,考查直线与椭圆的位置关系,考查弦长公式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目