题目内容
已知f (x)是定义在R上的不恒为零的函数,且对于任意的a、b∈R都满足f(a•b)=af(b)+bf(a).
(1)求f(0),f(1)的值;
(2)判断f (x)的奇偶性,并证明你的结论;
(3)若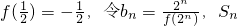 表示数列{bn}的前n项和.试问:是否存在关于n的整式g (n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g (n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
表示数列{bn}的前n项和.试问:是否存在关于n的整式g (n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g (n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
解:(1)令a=b=0,得f(0)=0•f(0)+0•f(0)=0.
令a=b=1,得f(1)=1•f(1)+1•f(1),∴f(1)=0.(2分)
(2)令a=b=-1,得f(1)=f[(-1)•(-1)]=-f(-1)-f(-1)=-2f(-1),∴f(-1)=0.
令a=-1,b=x,得f(-x)=f(-1•x)=-1•f(x)+x•f(-1)=-f(x)+0=-f(x).∴f(x)是奇函数.(5分)
(3)当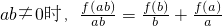 .
.
令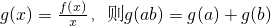 ,∴g(an)=ng(a).(7分)
,∴g(an)=ng(a).(7分)
∴f(an)=an•g(an)=n•an•g(a)=n•an-1•f(a).
∵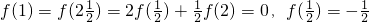
∴f(2)=2,
∴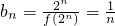 (9分)
(9分)
∴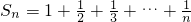 ,
,
∴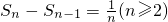
即nSn-(n-1)Sn-1=Sn-1+1,(11分)
∴(n-1)Sn-1-(n-2)Sn-2=Sn-2+1,…,2S2-S1=S1+1,
∴nSn-S1=S1+S2+…+Sn-1+n-1,
∴S1+S2+…Sn-1=nSn-n=(Sn-1)•n(n≥2)
∴g(n)=n.
故存在关于n的整式g (n)=n,使等式对于一切不小于2的自然数n恒成立 (13分)
分析:(1)令a=b=0,得f(0)=0•f(0)+0•f(0)=0,令a=b=1,得f(1)=1•f(1)+1•f(1),故可解;
(2)令a=b=-1,可得f(-1)=0;令a=-1,b=x,可得f(-x)=-f(x),故可得f(x)是奇函数;
(3)先可得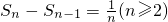 ,即nSn-(n-1)Sn-1=Sn-1+1,从而(n-1)Sn-1-(n-2)Sn-2=Sn-2+1,…,S2-S1=S1+1由此可得S1+S2+…Sn-1=nSn-n=(Sn-1)•n(n≥2),故可解.
,即nSn-(n-1)Sn-1=Sn-1+1,从而(n-1)Sn-1-(n-2)Sn-2=Sn-2+1,…,S2-S1=S1+1由此可得S1+S2+…Sn-1=nSn-n=(Sn-1)•n(n≥2),故可解.
点评:本题考查了数列与函数的综合运用,主要涉及了函数的赋值法,等差数列,函数的奇偶性及通项公式的计算等知识.
令a=b=1,得f(1)=1•f(1)+1•f(1),∴f(1)=0.(2分)
(2)令a=b=-1,得f(1)=f[(-1)•(-1)]=-f(-1)-f(-1)=-2f(-1),∴f(-1)=0.
令a=-1,b=x,得f(-x)=f(-1•x)=-1•f(x)+x•f(-1)=-f(x)+0=-f(x).∴f(x)是奇函数.(5分)
(3)当
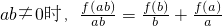 .
.令
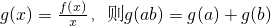 ,∴g(an)=ng(a).(7分)
,∴g(an)=ng(a).(7分)∴f(an)=an•g(an)=n•an•g(a)=n•an-1•f(a).
∵
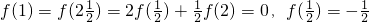
∴f(2)=2,
∴
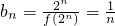 (9分)
(9分)∴
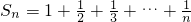 ,
,∴
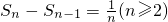
即nSn-(n-1)Sn-1=Sn-1+1,(11分)
∴(n-1)Sn-1-(n-2)Sn-2=Sn-2+1,…,2S2-S1=S1+1,
∴nSn-S1=S1+S2+…+Sn-1+n-1,
∴S1+S2+…Sn-1=nSn-n=(Sn-1)•n(n≥2)
∴g(n)=n.
故存在关于n的整式g (n)=n,使等式对于一切不小于2的自然数n恒成立 (13分)
分析:(1)令a=b=0,得f(0)=0•f(0)+0•f(0)=0,令a=b=1,得f(1)=1•f(1)+1•f(1),故可解;
(2)令a=b=-1,可得f(-1)=0;令a=-1,b=x,可得f(-x)=-f(x),故可得f(x)是奇函数;
(3)先可得
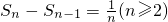 ,即nSn-(n-1)Sn-1=Sn-1+1,从而(n-1)Sn-1-(n-2)Sn-2=Sn-2+1,…,S2-S1=S1+1由此可得S1+S2+…Sn-1=nSn-n=(Sn-1)•n(n≥2),故可解.
,即nSn-(n-1)Sn-1=Sn-1+1,从而(n-1)Sn-1-(n-2)Sn-2=Sn-2+1,…,S2-S1=S1+1由此可得S1+S2+…Sn-1=nSn-n=(Sn-1)•n(n≥2),故可解.点评:本题考查了数列与函数的综合运用,主要涉及了函数的赋值法,等差数列,函数的奇偶性及通项公式的计算等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)是定义在R上的函数,并满足f(x)f(x+2)=-1,当1<x<2时,f(x)=x3+sin
x,则f(5.5)=( )
| π |
| 9 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|