Question

已知f（x）是定义在R上的奇函数，f（2）=0，[xf（x）]′＞0（x＞0），则不等式f（x）≤0的解集是

（-∞，-2]∪[0，2]

．

Answer 1

分析：构造函数F（x）=xf（x），利用函数F（x）的单调性研究函数f（x）≤0的解集问题．

解答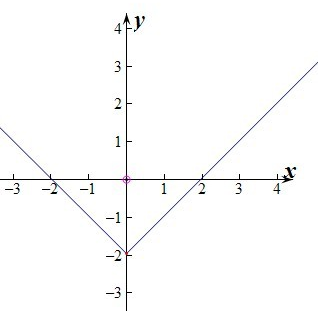：解：设F（x）=xf（x），因为f（x）是定义在R上的奇函数，所以F（x）为偶函数，
当x＞0时，[xf（x）]′＞0，即F（x）单调递增，因为f（2）=0，所以F（2）=0，F（-2）=0．
F（0）=0．
所以F（x）取值的草图为：（图象知体现单调性）．
当x＞0时，f（x）≤0与F（x）=xf（x）≤0同解，
由图象可知，此时0＜x≤2．
当x＜0时，f（x）≤0，则F（x）=xf（x）≥0，此时x≤-2．
当x=0时，f（0）=0≤0也成立．
综上不等式f（x）≤0的解为：0≤x≤2或x≤-2．
即不等式f（x）≤0的解集（-∞，-2]∪[0，2]．
故答案为：（-∞，-2]∪[0，2]．

点评：本题主要考查函数的单调性和导数之间的关系，要求熟练掌握函数单调性的应用，
构造函数F（x）=xf（x），利用F（x）的图象和性质是解决本题的关键，综合性较强．