题目内容
(理科)某中学有5名体育类考生要到某大学参加体育专业测试,学校指派一名教师带队,已知每位考生测试合格的概率都是 ,(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
,(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
(2)若5人中恰有r人合格的概率为 ,求r的值;
,求r的值;
(3)记测试合格的人数为ξ,求ξ的期望和方差.
解:(1)由题意可得:老师进行选择时共有6种不同的选法,体育教师不坐后排的不同选法有C31=3种,
记“体育教师不坐后排”为事件A,则 .-----(4分)
.-----(4分)
(2)每位考生测试合格的概率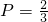 ,测试不合格的概率为
,测试不合格的概率为
则 ,即
,即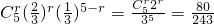 ,
,
∴C5r2r=80,解得:r=3,4.
(3)由题意可得:ξ~ ,
,
∴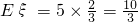 ,
, ----(12分)
----(12分)
分析:(1)由题意可得:老师进行选择时共有6种不同的选法,体育教师不坐后排的不同选法有C31=3种,进而得到答案.
(2)每位考生测试合格的概率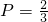 ,测试不合格的概率为
,测试不合格的概率为 ,则得到
,则得到 ,再解方程可得答案.
,再解方程可得答案.
(3)由题意可得:ξ~ ,进而根据二项分布的有关公式可得答案.
,进而根据二项分布的有关公式可得答案.
点评:解决此类问题的关键是熟练掌握等可能事件的概率与独立重复试验的概率公式,以及二项分布计算期望与方程的公式,即Eξ=np,Dξ=np(1-p),此题属于基础题.
记“体育教师不坐后排”为事件A,则
 .-----(4分)
.-----(4分)(2)每位考生测试合格的概率
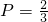 ,测试不合格的概率为
,测试不合格的概率为
则
 ,即
,即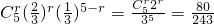 ,
,∴C5r2r=80,解得:r=3,4.
(3)由题意可得:ξ~
 ,
,∴
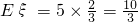 ,
, ----(12分)
----(12分)分析:(1)由题意可得:老师进行选择时共有6种不同的选法,体育教师不坐后排的不同选法有C31=3种,进而得到答案.
(2)每位考生测试合格的概率
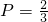 ,测试不合格的概率为
,测试不合格的概率为 ,则得到
,则得到 ,再解方程可得答案.
,再解方程可得答案.(3)由题意可得:ξ~
 ,进而根据二项分布的有关公式可得答案.
,进而根据二项分布的有关公式可得答案.点评:解决此类问题的关键是熟练掌握等可能事件的概率与独立重复试验的概率公式,以及二项分布计算期望与方程的公式,即Eξ=np,Dξ=np(1-p),此题属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ,(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
,(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;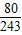 ,求r的值;
,求r的值;