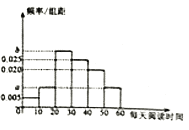
题目内容
【题目】已知符号函数sgnx= 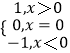 ,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则( )
,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则( )
A.sgn[g(x)]=sgnx
B.sgn[g(x)]=﹣sgnx
C.sgn[g(x)]=sgn[f(x)]
D.sgn[g(x)]=﹣sgn[f(x)]
【答案】B
【解析】解:由于本题是选择题,可以采用特殊法,符号函数sgnx= 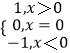 ,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),
,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),
不妨令f(x)=x,a=2,
则g(x)=f(x)﹣f(ax)=﹣x,
sgn[g(x)]=﹣sgnx.所以A不正确,B正确,
sgn[f(x)]=sgnx,C不正确;D正确;
对于D,令f(x)=x+1,a=2,
则g(x)=f(x)﹣f(ax)=﹣x,
sgn[f(x)]=sgn(x+1)= 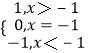 ;
;
sgn[g(x)]=sgn(﹣x)= 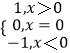 ,
,
﹣sgn[f(x)]=﹣sgn(x+1)= 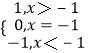 ;所以D不正确;
;所以D不正确;
故选:B.

练习册系列答案
相关题目