题目内容
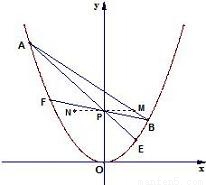 已知抛物线y=x2和三个点M(x,y)、P(0,y)、N(-x,y)(y≠x2,y>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F.
已知抛物线y=x2和三个点M(x,y)、P(0,y)、N(-x,y)(y≠x2,y>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F.(1)证明E、F、N三点共线;
(2)如果A、B、M、N四点共线,问:是否存在y,使以线段AB为直径的圆与抛物线有异于A、B的交点?如果存在,求出y的取值范围,并求出该交点到直线AB的距离;若不存在,请说明理由.
【答案】分析:(1)设出A,B,E,F的坐标,进而可表示出直线AB的方程,把点M代入,整理可得到y的表达式,进而把直线AP的方程与抛物线方程联立,利用韦达定理表示出xF和yF,xE和yE,将y的表达式代入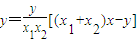 得y=y,判断出N点在直线EF上.
得y=y,判断出N点在直线EF上.
(2)已知A、B、M、N共线,可分别表示出A,B的坐标和以AB为直径的圆的方程,与抛物线方程联立求得y和y的关系要使圆与抛物线有异于A,B的交点判断y-1≥0,进而可推断出存在y≥1,使以AB为直径的圆与抛物线有异于A,B的交点T且yT=y-1进而求得交点T到AB的距离.
解答:(1)证明:设A(x1,x12)、B(x2,x22),E(xE,yE)、F(xF,yF)
则直线AB的方程: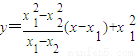
即:y=(x1+x2)x-x1x2
因M(x,y)在AB上,所以y=(x1+x2)x-x1x2①
又直线AP方程: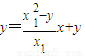
由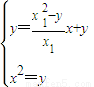 得:
得: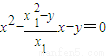
所以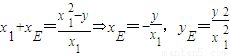
同理,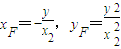
所以直线EF的方程:
令x=-x得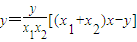
将①代入上式得y=y,即N点在直线EF上
所以E,F,N三点共线
(2)解:由已知A、B、M、N共线,所以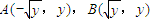
以AB为直径的圆的方程:x2+(y-y)2=y
由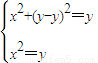 得y2-(2y-1)y+y2-y=0
得y2-(2y-1)y+y2-y=0
所以y=y(舍去),y=y-1
要使圆与抛物线有异于A,B的交点,则y-1≥0
所以存在y≥1,使以AB为直径的圆与抛物线有异于A,B的交点T(xT,yT)
则yT=y-1,所以交点T到AB的距离为y-yT=y-(y-1)=1
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的关键是充分发挥判别式和韦达定理在解题中的作用.
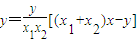 得y=y,判断出N点在直线EF上.
得y=y,判断出N点在直线EF上.(2)已知A、B、M、N共线,可分别表示出A,B的坐标和以AB为直径的圆的方程,与抛物线方程联立求得y和y的关系要使圆与抛物线有异于A,B的交点判断y-1≥0,进而可推断出存在y≥1,使以AB为直径的圆与抛物线有异于A,B的交点T且yT=y-1进而求得交点T到AB的距离.
解答:(1)证明:设A(x1,x12)、B(x2,x22),E(xE,yE)、F(xF,yF)
则直线AB的方程:
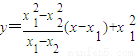
即:y=(x1+x2)x-x1x2
因M(x,y)在AB上,所以y=(x1+x2)x-x1x2①
又直线AP方程:
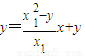
由
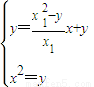 得:
得: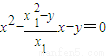
所以
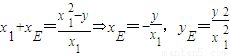
同理,
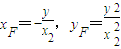
所以直线EF的方程:

令x=-x得
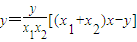
将①代入上式得y=y,即N点在直线EF上
所以E,F,N三点共线
(2)解:由已知A、B、M、N共线,所以
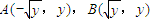
以AB为直径的圆的方程:x2+(y-y)2=y
由
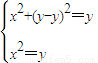 得y2-(2y-1)y+y2-y=0
得y2-(2y-1)y+y2-y=0所以y=y(舍去),y=y-1
要使圆与抛物线有异于A,B的交点,则y-1≥0
所以存在y≥1,使以AB为直径的圆与抛物线有异于A,B的交点T(xT,yT)
则yT=y-1,所以交点T到AB的距离为y-yT=y-(y-1)=1
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的关键是充分发挥判别式和韦达定理在解题中的作用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2上有一定点A(-1,1)和两动点P、Q,当PA⊥PQ时,点Q的横坐标取值范围是( )
| A、(-∞,-3] | B、[1,+∞) | C、[-3,1] | D、(-∞,-3]∪[1,+∞) |
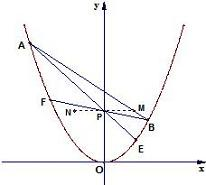 已知抛物线y=x2和三个点M(x0,y0)、P(0,y0)、N(-x0,y0)(y0≠x02,y0>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F.
已知抛物线y=x2和三个点M(x0,y0)、P(0,y0)、N(-x0,y0)(y0≠x02,y0>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F.