ЬтФПФкШн
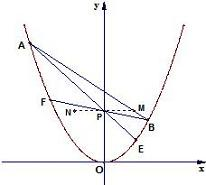 вбжЊХзЮяЯпy=x2КЭШ§ИіЕуMЃЈx0ЃЌy0ЃЉЁЂPЃЈ0ЃЌy0ЃЉЁЂNЃЈ-x0ЃЌy0ЃЉЃЈy0Ёйx02ЃЌy0ЃО0ЃЉЃЌЙ§ЕуMЕФвЛЬѕжБЯпНЛХзЮяЯпгкAЁЂBСНЕуЃЌAPЁЂBPЕФбгГЄЯпЗжБ№НЛЧњЯпCгкEЁЂFЃЎ
вбжЊХзЮяЯпy=x2КЭШ§ИіЕуMЃЈx0ЃЌy0ЃЉЁЂPЃЈ0ЃЌy0ЃЉЁЂNЃЈ-x0ЃЌy0ЃЉЃЈy0Ёйx02ЃЌy0ЃО0ЃЉЃЌЙ§ЕуMЕФвЛЬѕжБЯпНЛХзЮяЯпгкAЁЂBСНЕуЃЌAPЁЂBPЕФбгГЄЯпЗжБ№НЛЧњЯпCгкEЁЂFЃЎЃЈ1ЃЉжЄУїEЁЂFЁЂNШ§ЕуЙВЯпЃЛ
ЃЈ2ЃЉШчЙћAЁЂBЁЂMЁЂNЫФЕуЙВЯпЃЌЮЪЃКЪЧЗёДцдкy0ЃЌЪЙвдЯпЖЮABЮЊжБОЖЕФдВгыХзЮяЯпгавьгкAЁЂBЕФНЛЕуЃПШчЙћДцдкЃЌЧѓГіy0ЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіИУНЛЕуЕНжБЯпABЕФОрРыЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЗжЮіЃКЃЈ1ЃЉЩшГіAЃЌBЃЌEЃЌFЕФзјБъЃЌНјЖјПЩБэЪОГіжБЯпABЕФЗНГЬЃЌАбЕуMДњШыЃЌећРэПЩЕУЕНy0ЕФБэДяЪНЃЌНјЖјАбжБЯпAPЕФЗНГЬгыХзЮяЯпЗНГЬСЊСЂЃЌРћгУЮЄДяЖЈРэБэЪОГіxFКЭyFЃЌxEКЭyEЃЌНЋy0ЕФБэДяЪНДњШыy=
[(x1+x2)x0-y0]ЕУy=y0ЃЌХаЖЯГіNЕудкжБЯпEFЩЯЃЎ
ЃЈ2ЃЉвбжЊAЁЂBЁЂMЁЂNЙВЯпЃЌПЩЗжБ№БэЪОГіAЃЌBЕФзјБъКЭвдABЮЊжБОЖЕФдВЕФЗНГЬЃЌгыХзЮяЯпЗНГЬСЊСЂЧѓЕУy0КЭyЕФЙиЯЕвЊЪЙдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуХаЖЯy0-1Ён0ЃЌНјЖјПЩЭЦЖЯГіДцдкy0Ён1ЃЌЪЙвдABЮЊжБОЖЕФдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуTЧвyT=y0-1НјЖјЧѓЕУНЛЕуTЕНABЕФОрРыЃЎ
| y0 |
| x1x2 |
ЃЈ2ЃЉвбжЊAЁЂBЁЂMЁЂNЙВЯпЃЌПЩЗжБ№БэЪОГіAЃЌBЕФзјБъКЭвдABЮЊжБОЖЕФдВЕФЗНГЬЃЌгыХзЮяЯпЗНГЬСЊСЂЧѓЕУy0КЭyЕФЙиЯЕвЊЪЙдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуХаЖЯy0-1Ён0ЃЌНјЖјПЩЭЦЖЯГіДцдкy0Ён1ЃЌЪЙвдABЮЊжБОЖЕФдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуTЧвyT=y0-1НјЖјЧѓЕУНЛЕуTЕНABЕФОрРыЃЎ
НтД№ЃКЃЈ1ЃЉжЄУїЃКЩшAЃЈx1ЃЌx12ЃЉЁЂBЃЈx2ЃЌx22ЃЉЃЌEЃЈxEЃЌyEЃЉЁЂFЃЈxFЃЌyFЃЉ
дђжБЯпABЕФЗНГЬЃКy=
(x-x1)+
МДЃКy=ЃЈx1+x2ЃЉx-x1x2
вђMЃЈx0ЃЌy0ЃЉдкABЩЯЃЌЫљвдy0=ЃЈx1+x2ЃЉx0-x1x2Ђй
гжжБЯпAPЗНГЬЃКy=
x+y0
гЩ
ЕУЃКx2-
x-y0=0
Ыљвдx1+xE=
?xE=-
ЃЌyE=
ЭЌРэЃЌxF=-
ЃЌyF=
ЫљвджБЯпEFЕФЗНГЬЃКy=-(
)y0x-
Сюx=-x0ЕУy=
[(x1+x2)x0-y0]
НЋЂйДњШыЩЯЪНЕУy=y0ЃЌМДNЕудкжБЯпEFЩЯ
ЫљвдEЃЌFЃЌNШ§ЕуЙВЯп
ЃЈ2ЃЉНтЃКгЩвбжЊAЁЂBЁЂMЁЂNЙВЯпЃЌЫљвдA(-
ЃЌy0)ЃЌB(
ЃЌy0)
вдABЮЊжБОЖЕФдВЕФЗНГЬЃКx2+ЃЈy-y0ЃЉ2=y0
гЩ
ЕУy2-ЃЈ2y0-1ЃЉy+y02-y0=0
Ыљвдy=y0ЃЈЩсШЅЃЉЃЌy=y0-1
вЊЪЙдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуЃЌдђy0-1Ён0
ЫљвдДцдкy0Ён1ЃЌЪЙвдABЮЊжБОЖЕФдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуTЃЈxTЃЌyTЃЉ
дђyT=y0-1ЃЌЫљвдНЛЕуTЕНABЕФОрРыЮЊy0-yT=y0-ЃЈy0-1ЃЉ=1
дђжБЯпABЕФЗНГЬЃКy=
| ||||
| x1-x2 |
| x | 2 1 |
МДЃКy=ЃЈx1+x2ЃЉx-x1x2
вђMЃЈx0ЃЌy0ЃЉдкABЩЯЃЌЫљвдy0=ЃЈx1+x2ЃЉx0-x1x2Ђй
гжжБЯпAPЗНГЬЃКy=
| ||
| x1 |
гЩ
|
| ||
| x1 |
Ыљвдx1+xE=
| ||
| x1 |
| y0 |
| x1 |
| ||
|
ЭЌРэЃЌxF=-
| y0 |
| x2 |
| ||
|
ЫљвджБЯпEFЕФЗНГЬЃКy=-(
| x1+x2 |
| x1x2 |
| ||
| x1x2 |
Сюx=-x0ЕУy=
| y0 |
| x1x2 |
НЋЂйДњШыЩЯЪНЕУy=y0ЃЌМДNЕудкжБЯпEFЩЯ
ЫљвдEЃЌFЃЌNШ§ЕуЙВЯп
ЃЈ2ЃЉНтЃКгЩвбжЊAЁЂBЁЂMЁЂNЙВЯпЃЌЫљвдA(-
| y0 |
| y0 |
вдABЮЊжБОЖЕФдВЕФЗНГЬЃКx2+ЃЈy-y0ЃЉ2=y0
гЩ
|
Ыљвдy=y0ЃЈЩсШЅЃЉЃЌy=y0-1
вЊЪЙдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуЃЌдђy0-1Ён0
ЫљвдДцдкy0Ён1ЃЌЪЙвдABЮЊжБОЖЕФдВгыХзЮяЯпгавьгкAЃЌBЕФНЛЕуTЃЈxTЃЌyTЃЉ
дђyT=y0-1ЃЌЫљвдНЛЕуTЕНABЕФОрРыЮЊy0-yT=y0-ЃЈy0-1ЃЉ=1
ЕуЦРЃКБОЬтжївЊПМВщСЫжБЯпгыдВзЖЧњЯпЕФзлКЯЮЪЬтЃЎНтЬтЕФЙиМќЪЧГфЗжЗЂЛгХаБ№ЪНКЭЮЄДяЖЈРэдкНтЬтжаЕФзїгУЃЎ

СЗЯАВсЯЕСаД№АИ
 ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
ЯрЙиЬтФП
вбжЊХзЮяЯпy=x2ЩЯгавЛЖЈЕуAЃЈ-1ЃЌ1ЃЉКЭСНЖЏЕуPЁЂQЃЌЕБPAЁЭPQЪБЃЌЕуQЕФКсзјБъШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
| AЁЂЃЈ-ЁоЃЌ-3] | BЁЂ[1ЃЌ+ЁоЃЉ | CЁЂ[-3ЃЌ1] | DЁЂЃЈ-ЁоЃЌ-3]ЁШ[1ЃЌ+ЁоЃЉ |
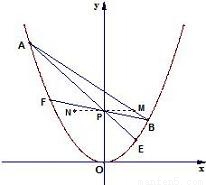 вбжЊХзЮяЯпy=x2КЭШ§ИіЕуMЃЈxЃЌyЃЉЁЂPЃЈ0ЃЌyЃЉЁЂNЃЈ-xЃЌyЃЉЃЈyЁйx2ЃЌyЃО0ЃЉЃЌЙ§ЕуMЕФвЛЬѕжБЯпНЛХзЮяЯпгкAЁЂBСНЕуЃЌAPЁЂBPЕФбгГЄЯпЗжБ№НЛЧњЯпCгкEЁЂFЃЎ
вбжЊХзЮяЯпy=x2КЭШ§ИіЕуMЃЈxЃЌyЃЉЁЂPЃЈ0ЃЌyЃЉЁЂNЃЈ-xЃЌyЃЉЃЈyЁйx2ЃЌyЃО0ЃЉЃЌЙ§ЕуMЕФвЛЬѕжБЯпНЛХзЮяЯпгкAЁЂBСНЕуЃЌAPЁЂBPЕФбгГЄЯпЗжБ№НЛЧњЯпCгкEЁЂFЃЎ