题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
若函数 ,如果存在给定的实数对
,如果存在给定的实数对 ,使得
,使得
恒成立,则称 为“
为“ 函数” .
函数” .
(1). 判断下列函数,是否为“ 函数”,并说明理由;
函数”,并说明理由;
① ②
② 
(2). 已知函数 是一个“
是一个“ 函数”,求出所有的有序实数对
函数”,求出所有的有序实数对 .
.
若函数
 ,如果存在给定的实数对
,如果存在给定的实数对 ,使得
,使得
恒成立,则称
 为“
为“ 函数” .
函数” .(1). 判断下列函数,是否为“
 函数”,并说明理由;
函数”,并说明理由;①
 ②
② 
(2). 已知函数
 是一个“
是一个“ 函数”,求出所有的有序实数对
函数”,求出所有的有序实数对 .
.(1)【解】
①(理)若 是“
是“ 函数”,则存在实数对
函数”,则存在实数对 ,使得
,使得 ,
,
即 时,对
时,对 恒成立 ……2分
恒成立 ……2分
而 最多有两个解,矛盾,
最多有两个解,矛盾,
因此 不是“
不是“ 函数” ……-3分
函数” ……-3分
(2)解 函数 是一个“
是一个“ 函数”
函数”
设有序实数对 满足,则
满足,则 恒成立
恒成立
当 时,
时, ,不是常数; ……8分
,不是常数; ……8分
因此 ,当
,当 时,
时,
则有 , ……10分
, ……10分
即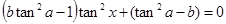 恒成立,
恒成立,
所以 ……13分
……13分
当 时,
时,
满足 是一个“
是一个“ 函数”的实数对
函数”的实数对
……14分
①(理)若
 是“
是“ 函数”,则存在实数对
函数”,则存在实数对 ,使得
,使得 ,
,即
 时,对
时,对 恒成立 ……2分
恒成立 ……2分而
 最多有两个解,矛盾,
最多有两个解,矛盾,因此
 不是“
不是“ 函数” ……-3分
函数” ……-3分(2)解 函数
 是一个“
是一个“ 函数”
函数”设有序实数对
 满足,则
满足,则 恒成立
恒成立当
 时,
时, ,不是常数; ……8分
,不是常数; ……8分因此
 ,当
,当 时,
时,则有
 , ……10分
, ……10分即
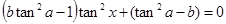 恒成立,
恒成立,所以
 ……13分
……13分当
 时,
时,
满足
 是一个“
是一个“ 函数”的实数对
函数”的实数对
……14分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,满足“对任意
中,满足“对任意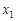 ,
, ,当
,当 时,
时, ”的是
”的是



 增加4万元,从第一年起每年蔬菜销售收入50万元.设
增加4万元,从第一年起每年蔬菜销售收入50万元.设 表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元).
表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元). (I)该厂从第几年开始盈利?
(I)该厂从第几年开始盈利? 的有序实数对,直线还是满足
的有序实数对,直线还是满足 的所有
的所有 组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点 定义它们之间的一种“距离”:
定义它们之间的一种“距离”: ,请解决以下问题:
,请解决以下问题:
 上一点
上一点 的距离到原点
的距离到原点 的“距离”;
的“距离”; 、
、 的“距离”
的“距离” ;
; 的“距离”均为
的“距离”均为  的“圆”方程;
的“圆”方程; 的垂直平分线的轨迹方程并画出大致图像.
的垂直平分线的轨迹方程并画出大致图像. ,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
,求经过这三个点确定的一个“圆”的方程,并画出大致图像; 
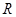 上的函数
上的函数 ,当
,当 时,
时, ,且对任意的
,且对任意的 满足
满足 (常数
(常数 ),则函数
),则函数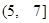 上的最小值是( )
上的最小值是( )



 ,
, 满足
满足 ,且
,且 ,则
,则 等于( )
等于( ) ,
, ,则
,则
 ,若
,若 互不相等,则
互不相等,则  的取值范围是( )
的取值范围是( )



 是定义在R上的函数,对一切
是定义在R上的函数,对一切 均有
均有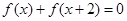 ,当
,当 时,
时, 则当
则当 时,
时,