题目内容
已知函数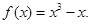
(I)求曲线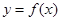 在
在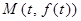 处的切线方程。
处的切线方程。
(II)设 如果过点
如果过点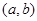 可作曲线
可作曲线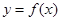 的三条切线,证明:
的三条切线,证明: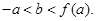
(I)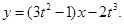
(II)通过研究函数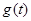 的极大值和极小值分别为
的极大值和极小值分别为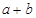 和
和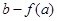 ,由
,由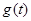 的单调性可知,
的单调性可知,
当极大值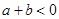 或极小值
或极小值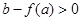 时,方程
时,方程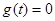 最多有一个实数根;
最多有一个实数根;
当极大值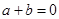 或极小值
或极小值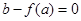 时,方程
时,方程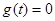 只有两个相异的实数根;
只有两个相异的实数根;
从而,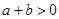 且
且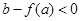 方程
方程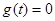 才有三个相异的实数根.即可得证
才有三个相异的实数根.即可得证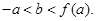
解析试题分析:(I)求函数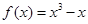 的导数:
的导数: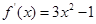 .
.
曲线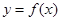 在点
在点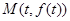 处的切线方程为
处的切线方程为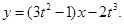
(II)如果有一切线过点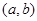 ,则存在
,则存在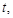 使得
使得 于是,若过点
于是,若过点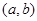 可作曲线
可作曲线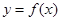 的三条切线,则转化为方程
的三条切线,则转化为方程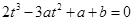 有三个相异的实数根。
有三个相异的实数根。
记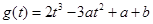 ,则
,则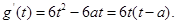
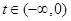 时,
时,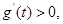 则
则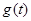 在此区间单调递增;
在此区间单调递增;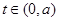 时,
时,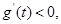 则
则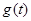 在此区间单调递减;
在此区间单调递减;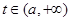 时,
时,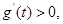 则
则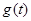 在此区间单调递增;
在此区间单调递增;
可求得函数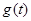 的极大值和极小值分别为
的极大值和极小值分别为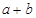 和
和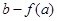 。
。
由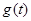 的单调性可知,
的单调性可知,
当极大值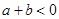 或极小值
或极小值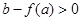 时,方程
时,方程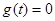 最多有一个实数根;
最多有一个实数根;
当极大值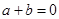 或极小值
或极小值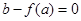 时,方程
时,方程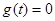 只有两个相异的实数根;
只有两个相异的实数根;
依题意: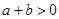 且
且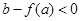 方程
方程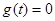 才有三个相异的实数根.
才有三个相异的实数根.
即可得证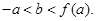
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性及极值,方程根的讨论。
点评:典型题,本题属于导数应用中的基本问题,通过求确定处导函数值,得到切线的斜率,进一步可求切线方程。讨论方程的根,可通过讨论函数的单调性及极值情况,认识切线特征,得到解题目的。

练习册系列答案
相关题目
 .(1)求函数
.(1)求函数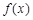 的单调区间;
的单调区间;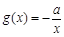 .若至少存在一个
.若至少存在一个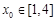 ,使得
,使得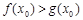 成立,求实数
成立,求实数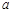 的取值范围.
的取值范围. ;
; 时,判断
时,判断 在定义域上的单调性;
在定义域上的单调性; 上的最小值.
上的最小值.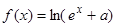 是实数集R上的奇函数,且
是实数集R上的奇函数,且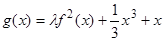 在R上为增函数。
在R上为增函数。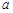 的值;
的值;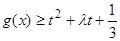 在
在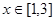 恒成立时的实数t的取值范围。
恒成立时的实数t的取值范围。
 ;
; 的切线方程。
的切线方程。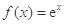 (
(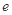 为自然对数的底数),
为自然对数的底数),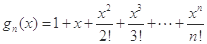 (
(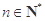 ).
).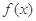
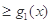 ;
;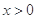 时,比较
时,比较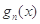 的大小,并说明理由;
的大小,并说明理由;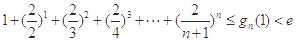 (
(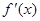 为f(x)的导函数,求证:
为f(x)的导函数,求证: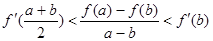
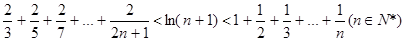
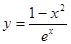 , 求
, 求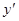
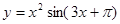 , 求
, 求 ..
..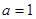 时,求
时,求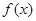 的单调区间;
的单调区间;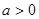 时,设
时,设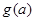 ,若
,若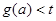 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.