题目内容
（本小题满分12分）
设函数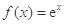
(
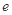为自然对数的底数)，
（
）．
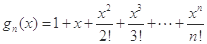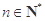（1）证明：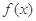
；
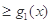（2）当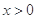
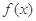时，比较与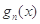
的大小，并说明理由；
（3）证明：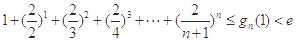
（）．
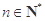（1）设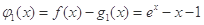
，即函数
在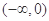
上单调递减，在
上单调递增，在
处取得唯一极小值。
（2）用数学归纳法证明即可；
（3）证明1：先证对任意正整数
，
，再证对任意正整数，
．
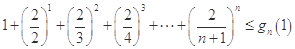
即要证明对任意正整数，不等式
（*）成立，以下可以数学归纳法证明。
解析
练习册系列答案
相关题目
题目内容
（本小题满分12分）
设函数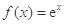(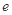为自然对数的底数)，（）．
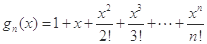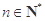（1）证明：；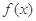
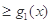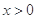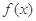（2）当时，比较与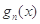的大小，并说明理由；
（3）证明：（）．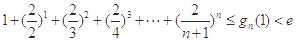
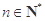（1）设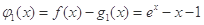，即函数在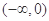上单调递减，在上单调递增，在处取得唯一极小值。
（2）用数学归纳法证明即可；
（3）证明1：先证对任意正整数，，再证对任意正整数，．
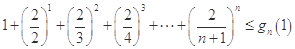
即要证明对任意正整数，不等式（*）成立，以下可以数学归纳法证明。
解析
，
，
内的一切实数
，不等式
恒成立，求实数
的取值范围；
时，求最大的正整数
，使得对
（
是自然对数的底数）内的任意
都有
成立；
．
＋
x＋1，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线垂直于y轴．(1)求a的值；(2)求函数f(x)的极值．
,
,设
．
的单调区间；
图像上任意一点
为切点的切线的斜率
恒成立，求实数
的最小值；
的图像与函数
的图像恰有四个不同的交点？若存在，求出实数m的取值范围；若不存在，说明理由。
在
处的切线方程。
如果过点
可作曲线
（其中e是自然对数的底数，k为正数）
在
处取得极值，且
，求
上的最大值.
在区间
上的最小值和最大值；
上是增函数，求实数a的取值范围。
.
在点
处与直线
相切，求
的值；
的极值点与极值.
在
上为增函数，求正实数
的取值范围；
，求证：