题目内容
已知函数y=sin
x+
cos
x,求:
(1)函数y的最大值,最小值及最小正周期;
(2)函数y的单调递增区间.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
(1)函数y的最大值,最小值及最小正周期;
(2)函数y的单调递增区间.
分析:(1)利用辅助角公式将y=sin
x+
cos
x转化为:y=2sin(
x+
),从而可求函数y的最大值,最小值及最小正周期;
(2)由2kπ-
≤
x+
≤2kπ+
(k∈Z)即可求得函数y的单调递增区间.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:解:(1)∵y=sin
x+
cos
x=2sin(
x+
),
∴ymax=2,ymin=-2,其最小正周期T=
=4π;
(2)由2kπ-
≤
x+
≤2kπ+
(k∈Z)得:4kπ-
≤x≤4kπ+
(k∈Z),
∴函数y的单调递增区间为[4kπ-
,4kπ+
](k∈Z).
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴ymax=2,ymin=-2,其最小正周期T=
| 2π | ||
|
(2)由2kπ-
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 3 |
| π |
| 3 |
∴函数y的单调递增区间为[4kπ-
| 5π |
| 3 |
| π |
| 3 |
点评:本题考查正弦函数的单调性及周期性与最值,着重考查正弦函数的图象与性质的灵活应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上单调递增,记M=sin1,N=sin1°,则M与N的大小关系是M________N.
上单调递增,记M=sin1,N=sin1°,则M与N的大小关系是M________N.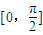 上单调递增,记M=sin1,N=sin1°,则M与N的大小关系是M N.
上单调递增,记M=sin1,N=sin1°,则M与N的大小关系是M N.