题目内容
已知实数 ,设函数
,设函数 ,
,  ,设
,设 分别为
分别为 图象上任意的点,若线段
图象上任意的点,若线段 长度的最小值为
长度的最小值为 ,则实数
,则实数 的值为( )
的值为( )
A. | B.2 | C. | D.2或 |
D
解析试题分析:分析两函数的图象可知, 分别为
分别为 图象上任意的点,若线段
图象上任意的点,若线段 长度的最小值为
长度的最小值为 ,存在两种可能,一是抛物线
,存在两种可能,一是抛物线 的顶点到y=-
的顶点到y=- 距离最小为
距离最小为 ,二是两函数切线斜率相等时,PQ长度最小为
,二是两函数切线斜率相等时,PQ长度最小为 ,在第一种情况下,抛物线
,在第一种情况下,抛物线 的顶点在x轴上,
的顶点在x轴上, ,解得a=2;结合选项分析可知,应选D。
,解得a=2;结合选项分析可知,应选D。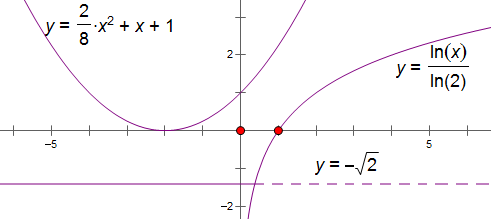
考点:二次函数的图象,对数函数的图象。
点评:中档题,通过分析两函数的图象,认识线段 长度的最小值为
长度的最小值为 时,存在两种可能,结合选项作出判断,省去繁琐的求导等计算活动。
时,存在两种可能,结合选项作出判断,省去繁琐的求导等计算活动。

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
已知a是函数 的零点,
的零点, a,则
a,则 的值满足( )
的值满足( )
A. =0 =0 | B. >0 >0 |
C. <0 <0 | D. 的符号不确定 的符号不确定 |
为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密、解密原理如下图: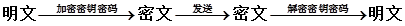
现在加密密钥为y=loga(x+2),如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到 密文为“4”,则解密后得到明文为
| A.12 | B.13 | C.14 | D.15 |
为了得到函数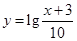 的图像,只需把函数
的图像,只需把函数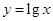 的图像上所有的点( )
的图像上所有的点( )
| A.向左平移3个单位长度,再向上平移1个单位长度 |
| B.向右平移3个单位长度,再向上平移1个单位长度 |
| C.向左平移3个单位长度,再向下平移1个单位长度 |
| D.向右平移3个单位长度,再向下平移1个单位长度 |
设a=log32,b=log52,c=log23,则( )
| A.a>c>b | B.b>c>a | C.c>b>a | D.c>a>b |
 ,则
,则 的图像大致为
的图像大致为
 对任意的
对任意的 都满足
都满足 ,当
,当 时,
时, ,若函数
,若函数 至少6个零点,则
至少6个零点,则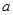 取值范围是( )
取值范围是( )



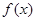 是定义在
是定义在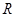 上的偶函数,且对任意的
上的偶函数,且对任意的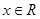 ,都有
,都有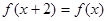 .当
.当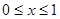 时,
时,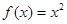 .若直线
.若直线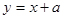 与函数
与函数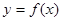 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数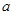 的值为( )
的值为( )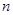
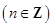

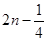
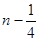
 ,形状为直角三角形的铁架框,有下列四种长度的铁管供选择,较经济(够用,又耗材最少)的是
,形状为直角三角形的铁架框,有下列四种长度的铁管供选择,较经济(够用,又耗材最少)的是 


