题目内容
函数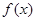 是定义在
是定义在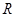 上的偶函数,且对任意的
上的偶函数,且对任意的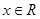 ,都有
,都有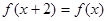 .当
.当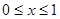 时,
时,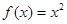 .若直线
.若直线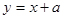 与函数
与函数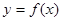 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数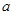 的值为( )
的值为( )
A.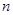 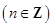 | B. 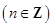 |
C. 或 或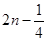 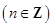 | D.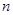 或 或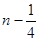 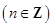 |
C
解析试题分析:因为,函数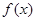 是定义在
是定义在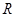 上的偶函数,且对任意的
上的偶函数,且对任意的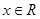 ,都有
,都有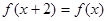 .所以,函数
.所以,函数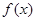 周期为2,又当
周期为2,又当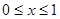 时,
时,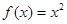 .结合其图象及直线
.结合其图象及直线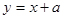 可知,直线
可知,直线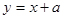 与函数
与函数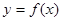 的图象有两个不同的公共点,包括相交、一切一交等两种情况,结合选项,选C。
的图象有两个不同的公共点,包括相交、一切一交等两种情况,结合选项,选C。
考点:函数的奇偶性、周期性,函数的图象。
点评:中档题,解函数不等式,往往需要将不等式具体化或利用函数的图象,结合函数的单调性。总之,要通过充分认识函数的特征,探寻解题的途径。

练习册系列答案
相关题目
设函数 ,
, ,则
,则 ( )
( )
| A.0 | B.38 | C.56 | D.112 |
若 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.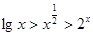 | B.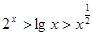 |
C.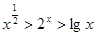 | D.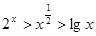 |
已知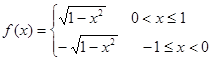 且
且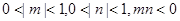 ,则使不等式
,则使不等式
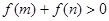 成立的m和n还应满足条件是( )
成立的m和n还应满足条件是( )
A.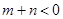 | B.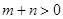 | C. | D.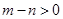 |
函数y= ln(1-x)的定义域为( )
ln(1-x)的定义域为( )
| A.(0,1) | B.[0,1) | C.(0,1] | D.[0,1) |
已知实数 ,设函数
,设函数 ,
,  ,设
,设 分别为
分别为 图象上任意的点,若线段
图象上任意的点,若线段 长度的最小值为
长度的最小值为 ,则实数
,则实数 的值为( )
的值为( )
A. | B.2 | C. | D.2或 |
已知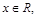 符号
符号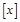 表示不超过
表示不超过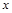 的最大整数,若函数
的最大整数,若函数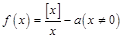 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( )
A. | B. |
C.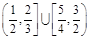 | D.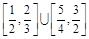 |
设函数f(x)= ,若f(x0)>1,则x0的取值范围为( )
,若f(x0)>1,则x0的取值范围为( )
A.(-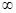 ,-1)∪(1,+ ,-1)∪(1,+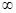 ) ) | B.(-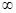 ,-1)∪[1,+ ,-1)∪[1,+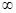 ) ) |
C.(-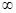 ,-3)∪(1,+ ,-3)∪(1,+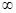 ) ) | D.(-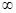 ,-3)∪[1,+ ,-3)∪[1,+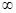 ) ) |
在数列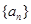 中,
中,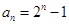 ,若一个7行12列的矩阵的第i行第j列的元素
,若一个7行12列的矩阵的第i行第j列的元素 ,(
,(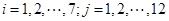 )则该矩阵元素能取到的不同数值的个数为( )
)则该矩阵元素能取到的不同数值的个数为( )
| A.18 | B.28 | C.48 | D.63 |