题目内容
设函数f(x)=x2+ax+b•2x(a≠0),若{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠φ,请你写出满足上述条件的一个函数f(x)的例子,如函数f(x)=________.
f(x)=x2+x(只要0<a<4且b=0即可)
分析:分析函数的结构特点,先由{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠∅,得到x2+ax+b•2x=(x2+ax+b•2x)22+a(x2+ax+b•2x)+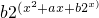 必有实数解,当x=0时,b=b2+ab+b•2b,b=0满足条件.然后进行化简,得到x2+ax=(x2+ax)2+a(x2+ax),当a=1时,(x2+x)2=0,x=0.由此得到满足上述条件的一个函数f(x)的例子f(x)=x2+x.
必有实数解,当x=0时,b=b2+ab+b•2b,b=0满足条件.然后进行化简,得到x2+ax=(x2+ax)2+a(x2+ax),当a=1时,(x2+x)2=0,x=0.由此得到满足上述条件的一个函数f(x)的例子f(x)=x2+x.
解答:∵函数f(x)=x2+ax+b•2x(a≠0),
{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠∅,
∴x2+ax+b•2x=(x2+ax+b•2x)22+a(x2+ax+b•2x)+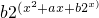 必有实数解,
必有实数解,
当x=0时,b=b2+ab+b•2b,
b=0满足条件.
把b=0代入x2+ax+b•2x=(x2+ax+b•2x)22+a(x2+ax+b•2x)+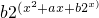 ,
,
得x2+ax=(x2+ax)2+a(x2+ax),
当a=1时,(x2+x)2=0,x=0.
综上所述,当a=1,b=0,f(x)=x2+x时,{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠φ.
故答案为:f(x)=x2+x.
(答案不唯一,(只要0<a<4且b=0即可).
点评:本题考查函数的解析式的求法和常规解法,解题时要认真审题,仔细解答,注意物特殊值的灵活运用.
分析:分析函数的结构特点,先由{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠∅,得到x2+ax+b•2x=(x2+ax+b•2x)22+a(x2+ax+b•2x)+
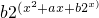 必有实数解,当x=0时,b=b2+ab+b•2b,b=0满足条件.然后进行化简,得到x2+ax=(x2+ax)2+a(x2+ax),当a=1时,(x2+x)2=0,x=0.由此得到满足上述条件的一个函数f(x)的例子f(x)=x2+x.
必有实数解,当x=0时,b=b2+ab+b•2b,b=0满足条件.然后进行化简,得到x2+ax=(x2+ax)2+a(x2+ax),当a=1时,(x2+x)2=0,x=0.由此得到满足上述条件的一个函数f(x)的例子f(x)=x2+x.解答:∵函数f(x)=x2+ax+b•2x(a≠0),
{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠∅,
∴x2+ax+b•2x=(x2+ax+b•2x)22+a(x2+ax+b•2x)+
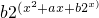 必有实数解,
必有实数解,当x=0时,b=b2+ab+b•2b,
b=0满足条件.
把b=0代入x2+ax+b•2x=(x2+ax+b•2x)22+a(x2+ax+b•2x)+
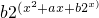 ,
,得x2+ax=(x2+ax)2+a(x2+ax),
当a=1时,(x2+x)2=0,x=0.
综上所述,当a=1,b=0,f(x)=x2+x时,{x|f(x)=0,x∈R}={x|f(f(x))=0,x∈R}≠φ.
故答案为:f(x)=x2+x.
(答案不唯一,(只要0<a<4且b=0即可).
点评:本题考查函数的解析式的求法和常规解法,解题时要认真审题,仔细解答,注意物特殊值的灵活运用.

练习册系列答案
相关题目