题目内容
设函数f（x）=x2-ax+a+3，g（x）=ax-2a．若存在x0∈R，使得f（x0）＜0与g（x0）＜0同时成立，则实数a的取值范围是分析：函数f（x）=x2-ax+a+3的图象恒过定点（1，4），g（x）=ax-2a的图象恒过定点（2，0），利用这两个定点，结合图象解决．
解答：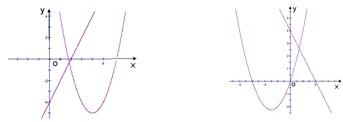
解：由f（x）=x2-ax+a+3知f（0）=a+3，f（1）=4，
又存在x0∈R，使得f（x0）＜0，
知△=a2-4（a+3）＞0即a＜-2或a＞6，
另g（x）=ax-2a中恒过（2，0），
故由函数的图象知：
①若a=0时，f（x）=x2-ax+a+3=x2+3恒大于0，显然不成立．
②若a＞0时，g（x0）＜0?x0＜2
?a＞7
③若a＜0时，g（x0）＜0?x0＞2
此时函数f（x）=x2-ax+a+3图象的对称轴x=
＜-1，
故函数在区间（
，+∞）上为增函数
又∵f（1）=4，
∴f（x0）＜0不成立．
故答案为：（7，+∞）．
解：由f（x）=x2-ax+a+3知f（0）=a+3，f（1）=4，又存在x0∈R，使得f（x0）＜0，
知△=a2-4（a+3）＞0即a＜-2或a＞6，
另g（x）=ax-2a中恒过（2，0），
故由函数的图象知：
①若a=0时，f（x）=x2-ax+a+3=x2+3恒大于0，显然不成立．
②若a＞0时，g（x0）＜0?x0＜2
|
③若a＜0时，g（x0）＜0?x0＞2
此时函数f（x）=x2-ax+a+3图象的对称轴x=
| a |
| 2 |
故函数在区间（
| a |
| 2 |
又∵f（1）=4，
∴f（x0）＜0不成立．
故答案为：（7，+∞）．
点评：充分挖掘题目中的隐含条件，结合图象法，可使问题的解决来得快捷．本题告诉我们，图解法对于解决存在性问题大有帮助．
练习册系列答案
相关题目