题目内容
在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝,第二件首饰是由6颗珠宝构成如图1所示的正六边形,第三件首饰是由15颗珠宝构成如图2所示的正六边形,第四件首饰是由28颗珠宝构成如图3所示的正六边形,第五件首饰是由45颗珠宝构成如图4所示的正六边形,以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断第6件首饰上应有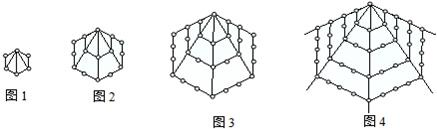
分析:由题意可知a1,a2,a3,a4,a5的值,则a2-a1=5,a3-a2=9,a4-a3=13,a5-a4=17,猜想a6-a5=21,从而得a6的值和an-an-1=4n-3;所以(a2-a1)+(a3-a2)+(a4-a3)+(a5-a4)+(a6-a5)+…+(an-an-1)=an-a1求得通项公式an,从而求得前n项和sn.
解答:解:由题意,知a1=1,a2=6,a3=15,a4=28,a5=45,a6=66,…;
∴a2-a1=5,a3-a2=9,a4-a3=13,a5-a4=17,a6-a5=21,…,an-an-1=4n-3;
∴(a2-a1)+(a3-a2)+(a4-a3)+(a5-a4)+(a6-a5)+…+(an-an-1)
=an-a1=5+9+13+17+21+…+(4n-3)=
=2n2-n-1;
∴an=2n2-n,其前n项和为sn=2(12+22+32+…+n2)-(1+2+3+…+n)
=2×
-
=
.
故答案为:66,
.
∴a2-a1=5,a3-a2=9,a4-a3=13,a5-a4=17,a6-a5=21,…,an-an-1=4n-3;
∴(a2-a1)+(a3-a2)+(a4-a3)+(a5-a4)+(a6-a5)+…+(an-an-1)
=an-a1=5+9+13+17+21+…+(4n-3)=
| (n-1)(5+4n-3) |
| 2 |
∴an=2n2-n,其前n项和为sn=2(12+22+32+…+n2)-(1+2+3+…+n)
=2×
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
| 4n3+3n2-n |
| 6 |
故答案为:66,
| 4n3+3n2-n |
| 6 |
点评:本题考查了数列的递推关系以及求和公式的综合应用,解题时要探究数列的递推关系,得出通项公式,并能正确求和.

练习册系列答案
相关题目

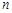 件首饰所用珠宝数为 颗.
件首饰所用珠宝数为 颗. 
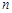 件首饰所用珠宝数为*****颗.
件首饰所用珠宝数为*****颗. 
