题目内容
(本小题满分12分)
已知椭圆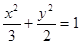 的左、右焦点分别为F1、F2.过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2.过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
(Ⅰ)设P点的坐标为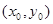 ,证明:
,证明: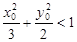 ;
;
(Ⅱ)求四边形ABCD的面积的最小值.
【答案】
(Ⅰ)椭圆的半焦距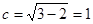 .
.
(Ⅰ)
(Ⅱ)四边形ABCD的面积的最小值为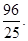
【解析】证明:
|
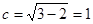 .
.
由AC⊥BD知点P在以线段F1F2为直径的圆上,
故 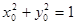 ,
,
所以, 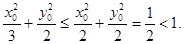
(Ⅱ)(i)当BD的斜率k存在且k≠0时,BD的方程为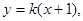 代入椭圆方程
代入椭圆方程
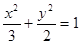 ,并化简得
,并化简得 
设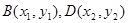 ,则
,则
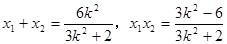
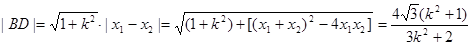
因为AC与BD相交于点P,且AC的斜率为 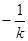 ,
,
所以, 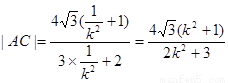
四边形ABCD的面积
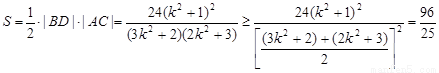
当k2=1时,上式取等号。
(ii)当BD的斜率k=0或斜率不存在时,四边形ABCD的面积S=4.
综上,四边形ABCD的面积的最小值为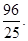

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
