题目内容
（2006•海淀区一模）已知四棱锥P-ABCD的底面是菱形，∠BCD=60°，PD⊥AD，点E是BC边的中点，（Ⅰ）求证：AD⊥平面PDE；
（Ⅱ）若二面角P-AD-C的大小等于60°，且AB=4，PD=
8
| ||
| 3 |
①求点P到平面ABCD的距离；
②求二面角P-AB-C的大小．
分析：（Ⅰ）连接BD，点E是BC边的中点，得出DE⊥BC，DE⊥AD再由DP⊥AD，得出AD⊥平面PDE．
（Ⅱ）DE⊥AD，PD⊥AD，∠PDE为二面角P-AD-C的平面角．∠PDE=60°．过P在平面PDE内做PK⊥DE于K，易证AD⊥PK．PK⊥面ABCD．PK为所求．
②先得出K为△BCD重心．连接BK，由△BCD为正三角形，得出BK为BP在面ABCD内的射影．从而PB⊥AB，所以∠PBK为二面角P-AB-C的平面角．RT△PKB中求解．
（Ⅱ）DE⊥AD，PD⊥AD，∠PDE为二面角P-AD-C的平面角．∠PDE=60°．过P在平面PDE内做PK⊥DE于K，易证AD⊥PK．PK⊥面ABCD．PK为所求．
②先得出K为△BCD重心．连接BK，由△BCD为正三角形，得出BK为BP在面ABCD内的射影．从而PB⊥AB，所以∠PBK为二面角P-AB-C的平面角．RT△PKB中求解．
解答：解：（Ⅰ）连接BD，底面ABCD是菱形，∠BDC=60°，∴△BCD是正三角形．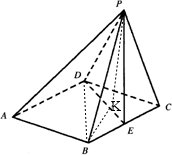
∵点E是BC边的中点，∴DE⊥BC，∵AD∥BC，∴DE⊥AD．∵DP⊥AD，DP∩AD=D，∴AD⊥平面PDE；
（Ⅱ）①∵DE⊥AD，PD⊥AD，∴∠PDE为二面角P-AD-C的平面角．，∴∠PDE=60°．
过P在平面PDE内做PK⊥DE于K，易证AD⊥PK．∴PK⊥面ABCD．∵PD=
，∴DK=
，PK=4
即点P到平面ABCD的距离是4．
②AB=4，∴DE=2
，∴DK=
DE，∴K为△BCD重心．
连接BK，∵△BCD为正三角形，所以BK为BP在面ABCD内的射影．∴PB⊥AB，∠PBK为二面角P-AB-C的平面角．
在RT△PKB中，tan∠PKB=
=
=
，∠PKB=
，二面角P-AB-C的大小为
∵点E是BC边的中点，∴DE⊥BC，∵AD∥BC，∴DE⊥AD．∵DP⊥AD，DP∩AD=D，∴AD⊥平面PDE；
（Ⅱ）①∵DE⊥AD，PD⊥AD，∴∠PDE为二面角P-AD-C的平面角．，∴∠PDE=60°．
过P在平面PDE内做PK⊥DE于K，易证AD⊥PK．∴PK⊥面ABCD．∵PD=
8
| ||
| 3 |
4
| ||
| 3 |
即点P到平面ABCD的距离是4．
②AB=4，∴DE=2
| 3 |
| 2 |
| 3 |
连接BK，∵△BCD为正三角形，所以BK为BP在面ABCD内的射影．∴PB⊥AB，∠PBK为二面角P-AB-C的平面角．
在RT△PKB中，tan∠PKB=
| PK |
| KB |
| PK |
| DK |
| 3 |
| π |
| 3 |
| π |
| 3 |
点评：本题考查空间直线、平面位置关系的判断，空间角大小求解，考查空间想象能力、推理论证、计算、转化能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目