题目内容
(本小题满分12分)
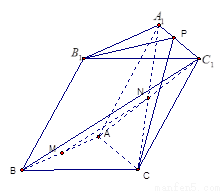
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1丄底面ABC.

(I)若M、N分别是AB,A1C的中点,求证:MN//平面BCC1B1
(II)若三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面 ABC所成的角为60°.问在线段A1C1上是否存在一点P,使得平面B1CP丄平面ACC1A1,若存在,求C1P与PA1的比值,若不存在,说明 理由.
【答案】
(1)利用线面平行的判定定理来证明即可。
(2)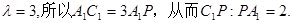
【解析】
试题分析:(Ⅰ)证明:连接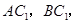 则
则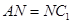 ,因为AM=MB,所以MN
,因为AM=MB,所以MN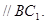 ……………2分
……………2分
又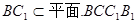 ,
,
所以MN//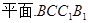 .…………4分
.…………4分
(Ⅱ)作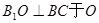 ,
,
因为面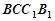
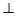 底面
底面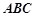
所以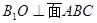
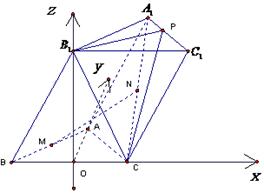
以O为原点,建立如图所示空间直角坐标系,则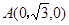 ,B(-1,0,0),C(1,0,0)
,B(-1,0,0),C(1,0,0)
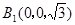 .由
.由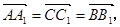 可求出
可求出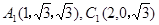
…………6分
设P(x,y,z),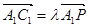
.解得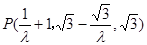 ,
,
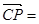
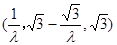 ,
,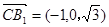 .
.
设平面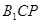 的法向量为
的法向量为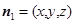
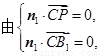 解得
解得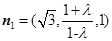 ………8分
………8分
同理可求出平面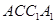 的法向量
的法向量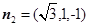 .…………10分
.…………10分
由面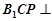 平面
平面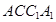 ,得
,得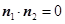 ,即
,即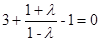
解得: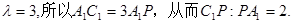 ………………12分
………………12分
考点:本试题考查了空间中的垂直和平行关系的证明。
点评:解决这类问题的关键是利用几何性质,线面的平行和垂直的判定定理和性质定理,来加以证明,或者利用空间向量的思想,建立直角坐标系,求点的坐标,运用向量法来得到求解,属于中档题。

练习册系列答案
相关题目