题目内容
（2011•渭南三模）设函数f(x)=
若f（-4）=f（0），f（-2）=0，则关于x的不等式f（x）≤1的解集为（ ）
|
分析：利用f（-4）=f（0），f（-2）=0，建立方程组
，解得b=c=4，由此能求出关于x的不等式f（x）≤1的解集．
|
解答：解：∵函数f(x)=
，
f（-4）=f（0），f（-2）=0，
∴
，
解得b=c=4，
∴f(x)=
，
∴当x＞0时，f（x）=-2≤1；
当x≤0时，
由f（x）=x2+4x+4≤1，
解得-3≤x≤-1．
综上所述，x的不等式f（x）≤1的解集为{x|x＞0，或-3≤x≤-1}．
故选C．
|
f（-4）=f（0），f（-2）=0，
∴
|
解得b=c=4，
∴f(x)=
|
∴当x＞0时，f（x）=-2≤1；
当x≤0时，
由f（x）=x2+4x+4≤1，
解得-3≤x≤-1．
综上所述，x的不等式f（x）≤1的解集为{x|x＞0，或-3≤x≤-1}．
故选C．
点评：本题考查二次函数的性质和应用，是基础题．解题时要认真审题，仔细解答，注意一元二次不等式的性质和应用．
练习册系列答案
相关题目
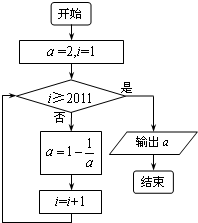（2011•渭南三模）已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
（2011•渭南三模）已知正三棱柱的侧面积为36，其三视图如图所示，则它的左视图的面积为（ ）