题目内容
【题目】设![]() 、
、![]() 为平面向量,若存在不全为零的实数λ,μ使得λ
为平面向量,若存在不全为零的实数λ,μ使得λ![]() μ
μ![]() 0,则称
0,则称![]() 、
、![]() 线性相关,下面的命题中,
线性相关,下面的命题中,![]() 、
、![]() 、
、![]() 均为已知平面M上的向量.
均为已知平面M上的向量.
①若![]() 2
2![]() ,则
,则![]() 、
、![]() 线性相关;
线性相关;
②若![]() 、
、![]() 为非零向量,且
为非零向量,且![]() ⊥
⊥![]() ,则
,则![]() 、
、![]() 线性相关;
线性相关;
③若![]() 、
、![]() 线性相关,
线性相关,![]() 、
、![]() 线性相关,则
线性相关,则![]() 、
、![]() 线性相关;
线性相关;
④向量![]() 、
、![]() 线性相关的充要条件是
线性相关的充要条件是![]() 、
、![]() 共线.
共线.
上述命题中正确的是 (写出所有正确命题的编号)
【答案】①④
【解析】
利用![]() 和
和 ![]() 线性相关 等价于
线性相关 等价于 ![]() 和
和 ![]() 是共线向量,故①正确,②不正确,④正确.通过举反例可得③不正确.
是共线向量,故①正确,②不正确,④正确.通过举反例可得③不正确.
解:若![]() 、
、![]() 线性相关,假设λ≠0,则
线性相关,假设λ≠0,则![]() ,故
,故 ![]() 和
和 ![]() 是共线向量.
是共线向量.
反之,若 ![]() 和
和 ![]() 是共线向量,则
是共线向量,则 ![]() ,即λ
,即λ![]() μ
μ![]() 0,故
0,故 ![]() 和
和 ![]() 线性相关.
线性相关.
故 ![]() 和
和 ![]() 线性相关 等价于
线性相关 等价于 ![]() 和
和 ![]() 是共线向量.
是共线向量.
①若![]() 2
2 ![]() ,则
,则 ![]() 2
2 ![]() 0,故
0,故 ![]() 和
和 ![]() 线性相关,故①正确.
线性相关,故①正确.
②若 ![]() 和
和 ![]() 为非零向量,
为非零向量,![]() ⊥
⊥![]() ,则
,则 ![]() 和
和 ![]() 不是共线向量,不能推出
不是共线向量,不能推出![]() 和
和 ![]() 线性相关,故②不正确.
线性相关,故②不正确.
③若![]() 和
和 ![]() 线性相关,则
线性相关,则 ![]() 和
和 ![]() 线性相关,不能推出若
线性相关,不能推出若![]() 和
和 ![]() 线性相关,例如当
线性相关,例如当![]() 时,
时,
![]() 和
和 ![]() 可以是任意的两个向量.故③不正确.
可以是任意的两个向量.故③不正确.
④向量![]() 和
和 ![]() 线性相关的充要条件是
线性相关的充要条件是 ![]() 和
和 ![]() 是共线向量,故④正确.
是共线向量,故④正确.
故答案为 ①④.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】为了推行“智慧课堂”教学,某老师分别用传统教学和“智慧课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期屮考试后,分别从两个班级屮各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以上统计数据填写下面![]() 列联表,并判断“成绩优良与教学方式是否有关”?
列联表,并判断“成绩优良与教学方式是否有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
| p>成绩不优良 | |||
总计 |
附: 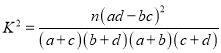 .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采川分层扣样的方法扣取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.