题目内容
动圆M经过定点F(1,0),且与直线x+1=0相切.
(1)求圆心M的轨迹C方程;
(2)直线l过定点F与曲线C交于A、B两点:
①若
=2
,求直线l的方程;
②若点T(t,0)始终在以AB为直径的圆内,求t的取值范围.
(1)求圆心M的轨迹C方程;
(2)直线l过定点F与曲线C交于A、B两点:
①若
| AF |
| FB |
②若点T(t,0)始终在以AB为直径的圆内,求t的取值范围.
分析:(1)由题意:M到点F(1,0)距离与M到直线x+1=0距离相等,利用抛物线的定义,可得圆心M的轨迹C方程;
(2))①设直线l:x=my+1,代入抛物线方程,利用韦达定理,及
=2
,可求直线l的方程;
②点T(t,0)始终在以AB为直径的圆内,等价于
•
<0,利用向量数量积公式,建立不等式,即可求t的取值范围.
(2))①设直线l:x=my+1,代入抛物线方程,利用韦达定理,及
| AF |
| FB |
②点T(t,0)始终在以AB为直径的圆内,等价于
| TA |
| TB |
解答:解:(1)由题意:M到点F(1,0)距离与M到直线x+1=0距离相等,所以点M的轨迹是以F为焦点,直线x+1=0为准线的抛物线,其方程为y2=4x
(2)①设直线l:x=my+1,代入抛物线方程得:y2-4my-4=0
设A(x1,y1),B(x2,y2)则y1+y2=4m,y1•y2=-4,
=(1-x1,-y1),
=(x2-1,y2)
由
=2
得-y1=2y2,代入y1+y2=4m,y1•y2=-4,解得:m=±
所以所求直线方程为x=±
y+1.
②
=(x1-t,y1),
=(x2-t,y2),
由题意,点T(t,0)始终在以AB为直径的圆内,∴
•
<0
即(x1-t)(x2-t)+y1y2<0,x1=my1+1,x2=my2+1,化简得:4tm2+4-(1-t)2>0对于任意的m∈R恒成立.
1°t=0满足;
2°t≠0,则t>0且4-(1-t)2>0,解得0<t<3.
综上知,t的取值范围为0≤t<3.
(2)①设直线l:x=my+1,代入抛物线方程得:y2-4my-4=0
设A(x1,y1),B(x2,y2)则y1+y2=4m,y1•y2=-4,
| AF |
| FB |
由
| AF |
| FB |
| ||
| 4 |
所以所求直线方程为x=±
| ||
| 4 |
②
| TA |
| TB |
由题意,点T(t,0)始终在以AB为直径的圆内,∴
| TA |
| TB |
即(x1-t)(x2-t)+y1y2<0,x1=my1+1,x2=my2+1,化简得:4tm2+4-(1-t)2>0对于任意的m∈R恒成立.
1°t=0满足;
2°t≠0,则t>0且4-(1-t)2>0,解得0<t<3.
综上知,t的取值范围为0≤t<3.
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查向量知识的运用,考查韦达定理,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
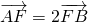 ,求直线l的方程;
,求直线l的方程;