题目内容
下列结论:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;②当x∈(1,+∞)时,函数
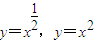 的图象都在直线y=x的上方;
的图象都在直线y=x的上方;③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx2-2x在区间(2+∞)内是增函数,则实数m的取值范围为
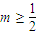 .
.其中,正确结论的个数是( )
A.1
B.2
C.3
D.4
【答案】分析:对于命题①要注意区分命题的否定形式与否命题的区别.
对于命题②抛物线和指数函数都在直线的上面,先判断它们没有交点,在判断是否同一个x它们的值都比直线上的取值大.
对于命题③由f(x)满足f(x+2)=-f(x),把f(6)化为-f(0),又根据奇数函数的性质在原点的函数值是0,可直接得到.
对于命题④根据抛物线的增减性,在对称轴两侧分别单调,即可得到答案.
解答:命题①“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”,是错误的因为否定形式只是对结论否定.
命题②当x∈(1,+∞)时,函数 的图象都在直线y=x的上方,根据图象的关系显然正确.
的图象都在直线y=x的上方,根据图象的关系显然正确.
命题③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
因为f(6)=-f(4)=f(2)=-f(0),又因为奇函数在原点的值为0,所以成立.
命题④抛物线在(2+∞)内是增函数,则开口向上所以m大于0,且对称轴小于等于2,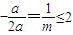 ,即得m的取值范所以命题正确.
,即得m的取值范所以命题正确.
故答案选择C.
点评:此题主要考查命题真假性问题,这类题目需要一个一个分析排除,虽然是选择题但涵盖信息量多,属于中档题目.
对于命题②抛物线和指数函数都在直线的上面,先判断它们没有交点,在判断是否同一个x它们的值都比直线上的取值大.
对于命题③由f(x)满足f(x+2)=-f(x),把f(6)化为-f(0),又根据奇数函数的性质在原点的函数值是0,可直接得到.
对于命题④根据抛物线的增减性,在对称轴两侧分别单调,即可得到答案.
解答:命题①“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”,是错误的因为否定形式只是对结论否定.
命题②当x∈(1,+∞)时,函数
 的图象都在直线y=x的上方,根据图象的关系显然正确.
的图象都在直线y=x的上方,根据图象的关系显然正确.命题③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
因为f(6)=-f(4)=f(2)=-f(0),又因为奇函数在原点的值为0,所以成立.
命题④抛物线在(2+∞)内是增函数,则开口向上所以m大于0,且对称轴小于等于2,
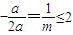 ,即得m的取值范所以命题正确.
,即得m的取值范所以命题正确.故答案选择C.
点评:此题主要考查命题真假性问题,这类题目需要一个一个分析排除,虽然是选择题但涵盖信息量多,属于中档题目.

练习册系列答案
相关题目
已知命题p:?x∈R,使sinx=
;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
①命题“p∧q”是真命题;
②命题“p∧¬q”是假命题;
③命题“¬p∨q”是真命题;
④命题“¬p∨¬q”是假命题.
其中正确的是( )
| ||
| 2 |
①命题“p∧q”是真命题;
②命题“p∧¬q”是假命题;
③命题“¬p∨q”是真命题;
④命题“¬p∨¬q”是假命题.
其中正确的是( )
| A、②③ | B、②④ | C、③④ | D、①②③ |